基本介紹
- 中文名:赫爾德不等式
- 外文名:Hölder inequality
- 類別:不等式
- 學科:數學
- 創建者:赫爾德
- 表現形式:離散形式和積分形式
離散的不等式
定義
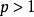
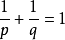
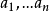

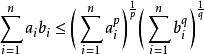
成立條件
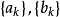
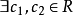
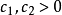


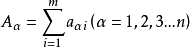
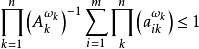
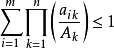

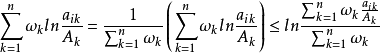
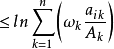
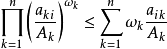
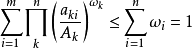
連續的不等式
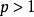
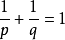
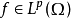
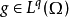
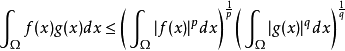
離散形式
內容
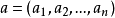
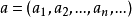
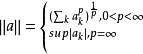
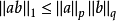
成立條件
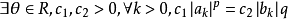
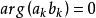
積分形式
內容
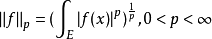
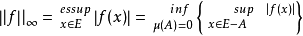
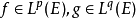

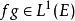
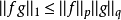
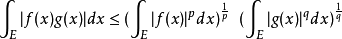
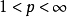
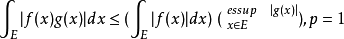
成立條件

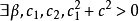

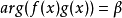
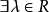
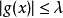
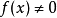
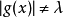
證明

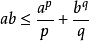
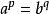
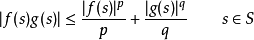
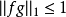
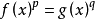
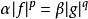

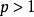
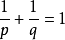
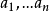

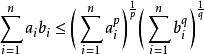
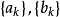
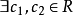
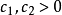


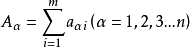
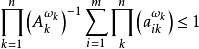
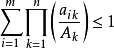

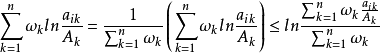
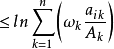
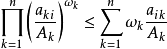
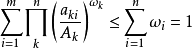
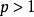
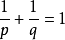
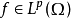
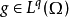
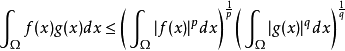
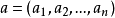
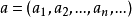
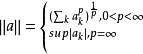
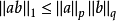
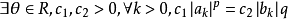
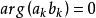
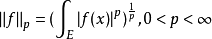
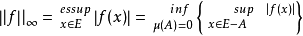
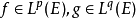

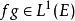
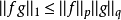
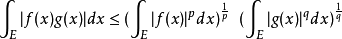
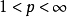
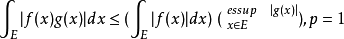

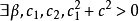

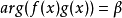
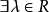
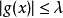
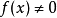
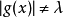

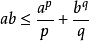
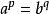
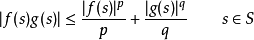
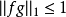
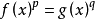
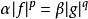
赫爾德不等式是數學分析的一條不等式,取名自奧圖·赫爾德(Otto Hölder)。這是一條揭示Lp空間相互關係的基本不等式。赫爾德不等式有許多證明,主要的想法是楊氏不...
反赫爾德不等式是與赫爾德不等式相反的不等式。迄今已建立了許多這類反赫爾德不等式。此外,調和分析中另有意義不同的同名不等式。...
逆向赫爾德不等式(inverse Holder inequality)是Ap類中權函式的一種重要性質。...... 逆向赫爾德不等式(inverse Holder inequality)是Ap類中權函式的一種重要性質。...
柯西-施瓦茨不等式是一個在眾多背景下都有套用的不等式,例如線性代數,數學分析,機率論,向量代數以及其他許多領域。它被認為是數學中最重要的不等式之一。此不等式...
數學上,柯西-施瓦茨不等式,又稱施瓦茨不等式或柯西-布尼亞科夫斯基-施瓦茨不等式,是一條很多場合都用得上的不等式;例如線性代數的矢量,數學分析的無窮級數和乘積的...
積分不等式是微積分學中的一類重要不等式,也為解決微分方程等方面的問題提供了 富有成效的理論工具。主要有楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式等...
在數學中,閔可夫斯基不等式(Minkowski inequality)是德國數學家赫爾曼·閔可夫斯基提出的重要不等式,該不等式表明Lp空間是一個賦范向量空間。閔可夫斯基的主要工作在...
哈代不等式(Hardy inequality)是與二重級數有關的不等式,即哈代(G.H.Hardy)研究二重級數時,於1920年建立的不等式。...
在數學中,閔可夫斯基不等式(Minkowski inequality)表明LP空間是一個賦范向量空間。...... 它可以用赫爾德不等式來證明。和赫爾德不等式一樣,閔可夫斯基不等式取可數...
赫爾德的著名成就包括:赫爾德不等式,若爾當-赫爾德定理,證明了每一滿足阿基米德性質的全序群都同構於實數的加法群的某一子群,200階以下簡單群的分類,發現了對稱群S6...
赫爾德的著名成就包括:赫爾德不等式,若爾當-赫爾德定理,證明了每一滿足阿基米德性質的全序群都同構於實數的加法群的某一子群,200階以下簡單群的分類,發現了對稱群S6...
《平均值不等式與柯西不等式》是2005年華東師範大學出版社出版的圖書,作者是李勝宏。...
《代數不等式》是2009年上海科技教育出版社出版的圖書,作者是陳計,季潮丞。...... 的不等式第五講 凸函式及一些複雜不等式 5.1 凸函式 5.2 赫爾德不等式 5....
《數學奧林匹克命題人講座·代數不等式》是2009年出版的圖書,作者是陳計。...... 第五講 凸函式及一些複雜不等式/134§5.1 凸函式/134§5.2 赫爾德不等式/1...
是一個線性映射,根據赫爾德不等式的極限情況, 作為泛函的範數和f一樣,這說明 是一個等距映射。此外還可以證明,對偶空間L(S,μ)中的任一線性泛函對偶空間G都能...
7.1.2 赫爾德不等式7.1.3 閔可夫斯基不等式7.2 向量範數7.2.1 向量範數7.2.2 向量範數的等價性7.3 矩陣範數7.3.1 矩陣範數...
,通過極限過程不難得到級數形式的赫爾德不等式從基本(或二重)赫爾德不等式(2) 與(4)出發,可以得到多重赫爾德不等式。定理3 設 是一組共軛指數,即 ,設 是 列...
作出了在數學分析中有廣泛套用的赫爾德不等式,包含了施瓦爾茲不等式對一般指數推廣的情形。研究了正規鏈理論,得出了在群論中有重要意義的若爾當一赫爾德序列和若爾當...
吳善和,1966年生,男,漢族,中共黨員。現任龍巖學院信息工程學院數學系教授、副院長。龍巖學院套用數學研究所所長、全國數學不等式研究會副理事長。...
2.福建省自然科學基金項目,2012J01014,冪指型平均的Schur凸性與精密型赫爾德不等式研究,2012/01-2014/12,3萬元,已結題,參加。3.資助省屬高校科研專項JK類,JK...
B.6 閔可夫斯基不等式與赫爾德不等式 387 B.7 算術平均值≥ 幾何平均值≥ 調和平均值 390 附錄C 機率論的補充知識 393 C.1 隨機變數的收斂 393 C.1.1 ...
權具有一個很重要的性質,即它滿足反向赫爾德不等式:若∈,1≤p0與常數,使得 Ap 對中的所有方塊成立。這一性質在近代偏微分方程理論中有重要的套用。 權是近代調...
8.2機率不等式 8.2.1馬爾可夫不等式和切爾諾夫不等式 8.2.2坎泰利不等式和切比雪夫不等式 8.3期望不等式 8.3.1琴生不等式 8.3.2赫爾德不等式和施瓦茨不等式...
