基本介紹
- 中文名:細拓撲
- 外文名:fine topology
- 領域:數學
- 性質:拓撲
- 定義:下半連續函式族確定的拓撲
- 子概念:細開集、細閉集、細閉包、細極限
概念,拓撲,下半連續函式,凸錐,子概念,開集,閉集,閉包,極限,
概念
細拓撲(fine topology)是由給定的下半連續函式族確定的、比原來拓撲細的一種拓撲。在非空集合Ω上賦予拓撲T,設Φ是一族從(Ω,T)到[0,+∞]的下半連續函式組成的凸錐(設+∞∈Φ),把形如:

的集全體記為S,那么S∪T所生成的拓撲T0是使Φ中每個函式都連續的最粗拓撲,稱之為(相對於Φ與T的)細拓撲。細拓撲下的開集、閉集、閉包、極限等分別稱為細開集、細閉集、細閉包、細極限等。在格林空間中,若不另作申明,則總認定Φ是非負超調和函式全體。一般地,談及細與瘦的概念時,都假定有了確定的Φ與T。
拓撲
1.X與空集都屬於T;
2.T中任意兩個成員的交屬於T;
3.T中任意多個成員的並屬於T;
則T稱為X上的一個拓撲。具有拓撲T的集合X稱為拓撲空間,記為(X,T)。
設T1與T2為集合X上的兩個拓撲。若有關係T1T2,則稱T1粗於T2,或T2細於T1。當X上的兩個拓撲相互之間沒有包含關係時,則稱它們是不可比較的。在集合X上,離散拓撲是最細的拓撲,平凡拓撲是最粗的拓撲。
下半連續函式
下半連續函式是指其上方圖形為閉集的函式。設X是拓撲空間,f:X→R∪{+∞},f≢+∞.若在x0∈X有網:
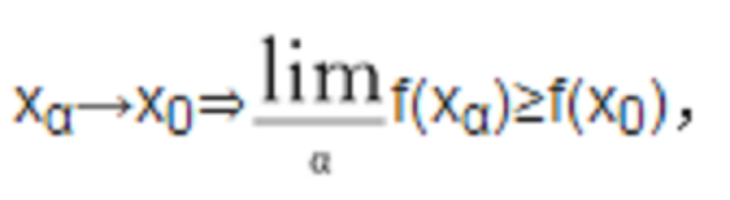
則稱f在x0為下半連續。若f在X中每點均為下半連續,則稱f在X上為下半連續。.f:X→R∪{+∞}為下半連續⇔ᗄc∈R,fc={x∈X|f(x)≤c}是X中的閉集⇔epi(f)={(x,t)∈X×R|f(x)≤t}是X×R中的閉集。若在上述定義中,將網xα換為序列xn,則得到f為依序列下半連續的概念。當然,在度量空間中,此二概念等價。當函式(-f):X→R∪{+∞}為下半連續時,則稱函式f:X→R∪{-∞}為上半連續。f在某點為連續,等價於f在此點既上半連續又下半連續。緊拓撲空間上的下半連續函式或序列緊拓撲空間上的依序列下半連續函式可達到其下確界。
凸錐
凸錐是一類特殊的凸集。實線性空間中既是凸集又是錐的集合稱為凸錐。凸錐C滿足C+C⊂C。對於X中的任何子集A,由它生成的凸錐是其元素的所有正線性組合的全體。而當A是凸集時,由A生成的凸錐就是λA。如果凸錐C滿足C∩(-C)={0},那么經常用它來定義實線性空間中的半序關係。對於x,y∈X, 定義x≥y為y∈x+C。則≥滿足:
1.x≥x.
2.x≥y,y≥x⇒x=y.
3.x≥y,y≥z⇒x≥z.
子概念
開集
閉集
閉集是拓撲空間的基本概念之一。拓撲空間中開集的補集稱為閉集。集合A是閉集若且唯若A等於它的閉包,或A的每個聚點都屬於A。拓撲空間X中閉集的全體稱為X的閉集系。由閉集的定義可得到與開集對偶的三條性質:
1.空集∅與X均為閉集。
2.任意多個閉集的交是閉集。
3.任意兩個閉集的並是閉集。
閉包
閉包是圖論的一個基本概念。指由一個圖所派生出的另一個圖。具體地說,一個圖G的閉包H是指符合下列條件包含邊最少的圖:G是H的支撐子圖;對於H上任何兩不相鄰節點v和w,都有ρH(v)+ρH(w)<n,這裡n表示H的階,ρH(v)和ρH(w)分別表示圖H上節點v和w的次。所謂閉包運算,就是如下從圖G得到它的閉包的遞歸過程:連通圖G上任何一對不相鄰且滿足ρG(u)+ρG(v)≥n的節點u和v連一邊,這裡ρG(u)和ρG(v)分別表示u,v在G上的次,而n表示G的階;對所得的圖仍進行這種運算,直到得到這樣的圖H,對於任何一對不相鄰節點u和v均有ρH(u)+ρH(v)<n成立。奧爾(Ore,O.)於1961年證明:若一個連通的簡單圖G,對於任何兩個不相鄰的節點,它們的次之和不小於G的階,則G必為哈密頓圖。稱節點次之和特別是兩個節點次之和所滿足的條件為奧爾型條件。所謂一個圖G的k閉包,是指符合下列條件且包含邊最少的圖H:G是H的支撐子圖;對於H上任何兩不相鄰節點v和u,都有ρH(v)+ρH(u)<k,0<k≤2n-4。於是,n階圖的閉包就是n閉包。這種與閉包運算類似的求一個圖的k閉包的過程稱為k閉包運算。設P是n階圖上的某種性質.在一個n階圖G上的兩個不相鄰的節點u,v,它們次之和ρG(u)+ρG(v)≥k.若G+(u,v)(即在G上加一條新邊所得的圖)具有性質P可以導出G本身也具有性質P,則稱P是k穩定的。若P是k穩定,則從一個圖的k閉包具有性質P可以導出它本身也有性質P.具有哈密頓圈的性質是n穩定的。
極限
數學分析的基本概念之一。由“無限逼近”思想而產生的一個重要數學概念。如果變數x按照某一規律變化,終於無限地逼近某一個常數c,則稱c為x的“極限”,記作limx=c或x→c。特別對於數列a1,a2,…an來說,如果當n無限增大時,數列的項an終於無限地接近一個常數c,則稱c為此數列的極限或稱此數列收斂於c,記作liman= c。極限思想在古希臘的窮竭法和中國古代的割圓術中已經萌芽。在牛頓的微積分中也含有極限思想。但是直到1821年,法國數學家柯西把極限概念建立在算術化的基礎上,人們對極限的理解才擺脫幾何直觀的局限。極限是一種方法,可用以計算函式的導數即變化率,或在整個分析中用來逼近一個真實量,例如曲線包圍的面積,定義它為某種矩形和所逼近的極限。圓內接正多邊形的邊數無限增加時,其面積的極限等於圓面積。極限的得出是“從有限中找到無限”(恩格斯)的認識方法在數學中的表現。只有無窮運算才會產生極限問題。極限總是和一個無限變化過程相聯繫。
