窮竭法的嚴格性是無可挑剔的。這對希臘數學家來說尤為可貴。事實上, 嚴格正是希臘幾何學的精神。窮竭法所完成的證明一般可分為兩個步驟: 首先是一個可稱之為“窮竭” 的逼近程式, 然後用“雙重歸謬法”(double reduetio ad absurdum)完成證明。
基本介紹
- 中文名:窮竭法
- 外文名:method of exhaustion
- 提出者:安提芬
- 改進者:歐多克斯
- 完善者:阿基米德
- 用途:確定面積和體積
歷史,發展,窮竭法與積分,相關研究,
歷史
有說布里松(Bryson或Bryso,450 B.C.前後)曾用過“窮竭”一詞 ,但沒有確切的證據,沒有一部古代可靠的權威典籍曾將他的名字與該方法聯繫起來。辛普利休斯(simplicJus,公元6世紀前半葉)曾描述過智人學派的安蒂豐(Antiphon,約430 B.C.)化圓為方的努力, 說他在圓內作一內接正多邊形,然後將邊數加倍得另一正多邊形。繼續此程式, 則圓與正多邊形之間的面積就越來越小, 當面積被窮竭時,他說他就用這種方法在圓內內接了一個正多邊形, 其邊與圓弧相合一致(因為他們很小), 由於我們可以作與任何正多邊形相等的正方形,因為多邊形已經作得相合於圓,我們將也能得到一個與圓相等的正方形”(SimpEcius語)。安蒂豐就這樣認為自己解決了希臘幾何作圖的三大問題之一一化圓為方。當然,安蒂豐沒有成功是明顯的,可我們從這裡得到的信息卻是模糊的,推測他是受了德謨克利特原子論學派的影響。另外, 所謂“相合一致” 是極為素樸的直覺觀念。事實上, 在此過程中, 多邊形永遠不能與圓相合。無論如何, 這種不斷作內接正多邊形的方式無疑成為後來窮竭法的濫觴。現在一般認為是歐多克索斯在前人工作的基礎上創造了窮竭法,首次用於數學證明,並取得了最初的成果。 圖1化圓為方探究
圖1化圓為方探究
 圖1化圓為方探究
圖1化圓為方探究歐多克索斯被他的同時代人譽為神明似的人。他的著作沒有流傳下來,所幸歐幾里得將其成果收入了“幾何原本 中。《幾何原本》 第Ⅻ篇中的一些命題是屬於歐多克索斯的。歐多克索斯一掃安蒂豐對割圓的補素模糊甚至是錯誤的觀念, 而將窮竭法建立在無限分割潛在可能性的基礎上。他並沒有使用諸如“無限” 、“(圓與正多邊形) 相合”之類的字眼。正由於此,有的數學史家認為“窮竭法避開了無限這個陷阱”。應該指出,窮竭法所避用的只是實無限罷了,這不僅因為當時缺少處理實無限的手段, 還由於亞里士多德在評述當時數學家的觀點時所說;事實上,他們不需要無限(按指實無限),也不使用無限。他們只是假定有限的直線能隨意延長而巳。因此, 從證明的需要來說, 只要有這種無限(按指潛無限)也就夠了。
歐多克索斯的這種潛無窮觀有其哲學淵源。在希臘哲學中,潛無窮觀念的初次表白是智人學派的安納薩戈拉斯(Anaxagoras,約499 B.C.~427 B.C.)作出的。安氏認為萬物都可以無限地分割,他以抽象的形式分析分割過程,而不管施行此過程的實際上的可能掛,將無限分割看作是潛在地可能宴現的過程。歐多克索斯正是吸收了安氏思想的合理內涵。
發展
作為一種嚴格的證明手段,窮竭法曾起過相當大的作用,但其局限性也是明顯的。首先是它建立在幾何直觀基礎上的雙重歸謬證明是煩瑣的, 因而給套用帶來了困難。其次它並不是一種適於發現新結果的方法。從發展眼光看,它必須進行修改以使其更為實用和簡便。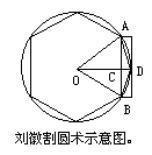 圖2劉徽割圓術示意圖
圖2劉徽割圓術示意圖
 圖2劉徽割圓術示意圖
圖2劉徽割圓術示意圖事實上,16、17世紀的數學家們巳認識到窮竭法邏輯上的優美與希臘幾何形式的不必要的煩瑣的差別, 而增長了純計算的興趣(這包括了對極限的模糊處理)。他們的探索推動了窮竭法向積分發展, 其間的種種努力促成了積分的誕生。大約有半打以上的數學家在這方面做出了實質性的貢獻。而這些工作差不多都來源於阿基米德的工作。
計算面積,體積以及求物體的重心等的重要的新方法是從恪改阿基米德的窮竭法開始的。
企圖修改窮竭法的途徑有兩種:一是對不同的直(曲)線形用不同類型的直(曲)邊形去逼近, 而l7世紀的數學家則採用了系統的程式'在老方法中用到雙重歸謬的地方,使逼近程式模糊地成為無窮,當時並沒有明顯地從極限上著想。後一條新途徑是斯蒂文(Simon Stevin)於1586年(即萊布尼茲於1684年和牛頓1687年分別首次發表他們的微積分方面著作前一個世紀)在他的《靜力學》(Statics)中提出的 後來有許多追隨者, 包括費馬在內。斯蒂文的步驟向極限方法的形成邁進了一步。當然當時的極限觀念是模糊的,但數學家們採用的不嚴格的外理方法卻得到了豐富的成果,如克卜勒、卡瓦列里。其時似乎沒有數學家顧慮到其嚴格的基礎問題。卡瓦列里就曾說過: “嚴格是哲學所關心的,而不是幾何學所關心的事情 。”
直到二百年後, 在柯西等人那裡分析學才又重新獲得了它的嚴格性。這種螺旋式上升正是事物發展的一般道路。在向積分的發展方向上,克卜勒、費馬、格雷戈里、卡瓦列里、瓦利斯等人都做出了自己的貢獻。到萊布尼茲及牛頓創立了微積分後,窮竭法使被根本地修改了。今天, 窮竭法巳成了歷史的名詞, 但歷史不應該忘記它。
窮竭法與積分
如所周知,將積分定義為和的極限是柯西給出的。一般認為他的定義是受到教學上用矩形逼近直線形面積啟發的。至於他是否受到希臘數學家的影響、影響多大我們不得而知。但無論如何, 儘管窮竭法的推證是幾何的而非算術的。但是,窮竭法中並沒有顯示出積分的法則,它只是積分的一種簡單情形。這裡的懸殊是觀念性的,而不僅僅廷辭彙與相對難易的問題 雖然知道一種技巧與將此技巧一般化之間差別不是太大, 但是積分法則是依賴於整套極限理論的, 這是窮竭法所不能企及的。但我們仍然可以說,窮竭法含有原始的積分思想,它的思想巳深深地滲透到了其後的數學中。
相關研究
古希臘的安提芬(Antiphon 480-403BC)最早表述了窮竭法,他在研究“化圓為方”問題時,提出了使用圓內接正多邊形面積“窮竭”圓面積的思想。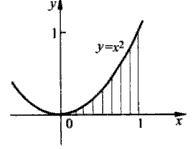 圖3化圓為方探究
圖3化圓為方探究
 圖3化圓為方探究
圖3化圓為方探究後來,古希臘數學家歐多克斯(Eudoxus of Cnidus, 408-355 BC)改進了安提芬的窮竭法。將其定義為:“(任意給定2個正的量)在一個量中減去比其一半還大的量,不斷重複這個過程,可以使剩下的量變得任意小”。
用現代語言描述是:
任意給定兩個正的量b<a, 從a 減去λa ,λa<1/2 , 則必可已找到一個整數n ,使(1-λ)n a<b。
例如,計算y=x2與x軸在x=0和x=1之間圍成的曲邊三角形的面積,把底邊[0,1]分成n等分,分點分別是1/n,2/n,…(n-1)/n,然後在每個分點處作底邊的垂線,這樣曲邊三角形被分成了n個窄條,對每個窄條,近似用矩形條替代。每個矩形的底寬1/n,高(i/n)2(i=0,1,2,…,n-1),把這些矩形條加起來,得到S的近似Sn:
Sn=0·(1/n)+(1/n)2·(1/n)+(2/n)2·(1/n)+…+[(n-1)/n]2·(1/n)=1/n3·[n(n+1)(2n+1)/6]=1/6·(1+1/n)(2+1/n)
對每個n,都可以算出相應的Sn的值,一方面,隨著n的增大Sn的值,來越接近S。但另一方面,所得的Sn始終都是S的近似值,為了得到S的精確值,使n無限制的增大,從幾何上看,面積Sn的那個多邊形越來越貼近曲邊三角形,即阿基米德所說的窮竭曲邊三角形,從數值上看,Sn無限接近一個確定的數,這個數就是曲邊三角形的面積S,這個數等於1/3,當年,阿基米德就是通過這個方法求得結果。
用窮竭法計算曲邊形的面積時,對不同的曲邊形,採用不同的直邊形去逼近。並且計算的過程中採用了特殊的技巧,因而不具有一般性,無法向一般的曲邊形推廣。
