基本介紹
- 中文名:濾子
- 外文名:filter
- 屬性:一類集族
- 創始人:昂利·嘉當
- 引進時間:1937年
定義,相關概念,定義1,定義2,定義3,相關定理,定理1,定理2,定理3,定理4,定理5,定理6,定理7,定理8,
定義
濾子: 設 是X的非空子集族,滿足:
是X的非空子集族,滿足:

(1) ;
;

(2)若 .則
.則 ;
;


(3)若 ,則
,則 。
。


則稱 為一個濾子(filter)。
為一個濾子(filter)。

濾子基: 設 為X的非空子集族,若它滿足
為X的非空子集族,若它滿足




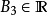
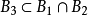
則稱 為X的一個濾子基。
為X的一個濾子基。

例1 設 是一個點網,
是一個點網,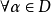 ,令
,令

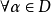

則 是一個濾子基。事實上,對於任意兩個
是一個濾子基。事實上,對於任意兩個 ,由於D是定向集,故存在一個
,由於D是定向集,故存在一個 ,使得
,使得 ,容易看出,
,容易看出, 。同時,每個
。同時,每個 顯然非空,因此
顯然非空,因此 是一個濾子基,這裡的集合
是一個濾子基,這裡的集合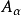 通常稱為由
通常稱為由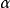 確定的終止集,而
確定的終止集,而 則稱為由
則稱為由 確定的濾子基。
確定的濾子基。







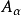
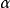


相關概念
定義1
定義2
設 為拓撲空間X的一個濾子,
為拓撲空間X的一個濾子,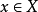 .如果
.如果 ,都有
,都有 ,則稱x為
,則稱x為 的聚點。濾子
的聚點。濾子 的聚點全體構成的集合記作adh
的聚點全體構成的集合記作adh 。如果對於
。如果對於 ,則稱x為
,則稱x為 的極限,此時也稱
的極限,此時也稱 在X中收斂於x,
在X中收斂於x, 在X中的全體極限構成的集合記作lim
在X中的全體極限構成的集合記作lim 。
。

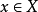










定義3
設 拓撲空間X的兩個濾子,若
拓撲空間X的兩個濾子,若 ,則稱
,則稱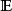 比
比 小(粗,或弱),也稱
小(粗,或弱),也稱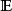 比
比 大(細,或強)。
大(細,或強)。


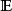

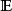

相關定理
定理1
設 和
和 是空間X的兩個濾子基,則
是空間X的兩個濾子基,則


(1) 是一個濾子基;
是一個濾子基;

(2)如果每個 ,則
,則 是一個濾子基;
是一個濾子基;


(3)對每個有限子集族 ,存在一個
,存在一個 使得
使得



例2 (1)設A是拓撲空間X的一個非空集合,則 顯然是一個濾子基。如果
顯然是一個濾子基。如果 ,則
,則 在X中收斂於a,如果
在X中收斂於a,如果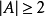 ,則每個
,則每個 都是
都是 的聚點。
的聚點。



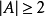


(2)不難驗證,拓撲空間X中點z的鄰域系N(x)是一個濾子,稱為鄰域濾子,它當然收斂於x,同時也以x作為聚點。
定理2
設 為拓撲空間X的一個濾子,則
為拓撲空間X的一個濾子,則 。
。


定理3
設 拓撲空間X的一個濾子,則
拓撲空間X的一個濾子,則 。
。


這一點從 的定義即可看出。
的定義即可看出。

定理4
如果 為Hausdorff空間X的一個收斂濾子,則
為Hausdorff空間X的一個收斂濾子,則 是單點集,且有關係式
是單點集,且有關係式



例2 考慮Sierpinski空間 是一個濾子,且不難驗證,
是一個濾子,且不難驗證, 既收斂於0,也收斂於1。
既收斂於0,也收斂於1。


下面這個定理建立了點網和濾子之間的關係。
定理5
(1)設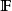 為拓撲空間X的一個濾子,則存在X中的點網
為拓撲空間X的一個濾子,則存在X中的點網 使得
使得
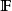


(2)設 是X中的任一點網,則存在X的一個濾子
是X中的任一點網,則存在X的一個濾子 使得
使得



這個定理表明,在描述收斂性方面,點網與濾子有著相同的作用,但是,對於一個給定的情形,往往其中一種描述會優於另一種描述,或者說,其中一種描述會比另一種描述更為方便。
由定理5,容易得到下面兩個定理,其證明較為簡單。
定理6
設 為拓撲空間X的一個濾子,則
為拓撲空間X的一個濾子,則 中有一個
中有一個 更粗的濾子
更粗的濾子 收斂於x。
收斂於x。




定理7
拓撲空間X是Hausdorff空間 X中的收斂濾子只有一個極限。
X中的收斂濾子只有一個極限。

由定理5和定理1容易得到下面的定理。






