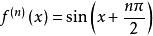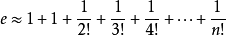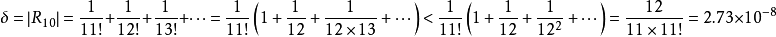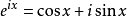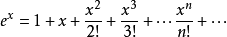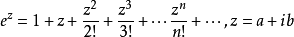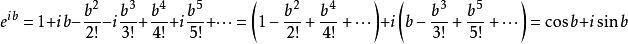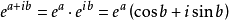歷史發展
泰勒簡介
18世紀早期
英國牛頓學派最優秀代表人物之一的英國數學家泰勒(Brook Taylor),於1685年8月18日在英格蘭德爾塞克斯郡的
埃德蒙頓市出生。1701年,泰勒進
劍橋大學的聖約翰學院學習。1709年後移居
倫敦,獲得法學學士學位。1712年當選為
英國皇家學會會員,同年進入促裁牛頓和萊布尼茲發明微積分優先權爭論的委員會。並於兩年後獲法學博士學位。從1714年起擔任皇家學會第一秘書,1718年以健康為由辭去這一職務。1717年,他以泰勒定理求解了數值方程。最後在1731年12月29日於
倫敦逝世。
泰勒以微積分學中將
函式展開成無窮
級數的定理著稱於世。這條定理大致可以敘述為:函式在一個點的鄰域內的值可以用函式在該點的值及各階
導數值組成的無窮級數表示出來。然而,在半個世紀裡,數學家們並沒有認識到泰勒定理的重大價值。這一重大價值是後來由
拉格朗日發現的,他把這一定理刻畫為微積分的基本定理。泰勒定理的嚴格證明是在定理誕生一個世紀之後,由柯西給出的。
泰勒定理開創了有限差分理論,使任何單變數函式都可展成
冪級數;同時亦使
泰勒成了有限差分理論的奠基者。泰勒於書中還討論了
微積分對一系列物理問題之套用,其中以有關弦的橫向振動之結果尤為重要。他透過求解方程導出了基本頻率公式,開創了研究弦振問題之先河。此外,此書還包括了他於數學上之其他創造性工作,如論述常
微分方程的奇異解,曲率問題之研究等。
發展過程
後來,
亞里士多德對芝諾悖論在哲學上進行了反駁,直到
德謨克利特以及後來的
阿基米德進行研究,此部分數學內容才得到解決。阿基米德套用
窮舉法使得一個無窮級數能夠被逐步的細分,得到了有限的結果。
17世紀,詹姆斯·格雷果里同樣繼續著這方面的研究,並且發表了若干
麥克勞林級數。直到1712年,英國
牛頓學派最優秀代表人物之一的數學家泰勒提出了一個通用的方法,這就是為人們所熟知的泰勒級數;
愛丁堡大學的
科林·麥克勞林教授發現了泰勒級數的特例,稱為
麥克勞林級數。
公式形式
泰勒公式形式
泰勒公式是將一個在x=x
0處具有n階導數的函式f(x)利用關於(x-x
0)的n次
多項式來逼近函式的方法。
若函式f(x)在包含x
0的某個閉區間[a,b]上具有n階導數,且在開區間(a,b)上具有(n+1)階
導數,則對
閉區間[a,b]上任意一點x,成立下式:
其中,表示f(x)的n階導數,等號後的多項式稱為函式f(x)在x0處的泰勒展開式,剩餘的Rn(x)是泰勒公式的餘項,是(x-x0)n的高階無窮小。
 泰勒公式
泰勒公式餘項
泰勒公式的餘項Rn(x)可以寫成以下幾種不同的形式:
1、佩亞諾(Peano)餘項:
這裡只需要n階導數存在。
2、施勒米爾希-羅什(Schlomilch-Roche)餘項:
其中θ∈(0,1),p為任意正實數。(注意到p=n+1與p=1分別對應拉格朗日餘項與柯西餘項)
其中θ∈(0,1)。
4、柯西(Cauchy)餘項:
其中θ∈(0,1)。
5、積分餘項:
其中以上諸多餘項事實上很多是等價的。
帶佩亞諾餘項
以下列舉一些常用函式的泰勒公式:
驗證推導
公式推導
於是:
其中誤差α是在Δx→0即x→x0的前提下才趨向於0,所以在近似計算中往往不夠精確。於是我們需要一個能夠足夠精確的且能估計出誤差的多項式:
來近似地表示函式f(x)且要寫出其誤差f(x)-P(x)的具體表達式。設函式P(x)滿足:
於是可以依次求出A0、A1、A2、……、An,顯然有:
至此,多項的各項係數都已求出,得:
以上就是函式的泰勒展開式。
接下來就要求誤差的具體表達式了。設,令得到:
進而:
其中θ1在x和x0之間;
其中θ2在θ1和x0之間;
連續使用n+1次後得到:
其中θ在x和x0之間;
同時:
進而:
綜上可得:
一般來說展開函式時都是為了計算的需要,故x往往要取一個定值,此時也可把Rn(x)寫為Rn。
麥克勞林展開
函式的麥克勞林展開指上面泰勒公式中x0取0的情況,即是泰勒公式的特殊形式,若f(x)在x=0處n階連續可導,則下式成立:
其中表示f(x)的n階導數。
當
,其中δ在0與x之間時,公式稱為拉格朗日型餘項的n階麥克勞林公式。
當
, 且n階導數存在時,公式稱為帶佩亞諾型的n階麥克勞林公式。
 近似表達正弦函式
近似表達正弦函式公式套用
實際套用中,泰勒公式需要截斷,只取有限項,一個函式的有限項的
泰勒級數叫做泰勒展開式。泰勒公式的餘項可以用於估算這種近似的誤差。
泰勒展開式的重要性體現在以下五個方面:
1、冪級數的求導和積分可以逐項進行,因此求和函式相對比較容易。
2、一個
解析函式可被延伸為一個定義在複平面上的一個開片上的解析函式,並使得複分析這種手法可行。
3、泰勒級數可以用來近似計算函式的值,並估計誤差。
實例
例1、在x=0處展開三角函式y=sinx和y=cosx。
解:根據導數表得:
顯然y=sinx在x=0處具有任意階導數。
根據麥克勞林公式:
類似地,可以展開y=cosx。
例2、計算近似值,並估計誤差。
當x=1時:
取n=10,即可算出近似值e≈2.7182818。
證明:
將該式子擴展到複數系內以定義指數函式,得到
特別地,當上式z=ib時,有
把上面的b換成x,就得到了歐拉公式。
由歐拉公式,對任意一個複數z=a+ib,有
即複數z的指數函式依然是一個複數,這個複數的模r=ea,幅角θ=b。
若b=0,則ez=ea(cos0+isin0)=ea(1+0)=ea,與實變函式f(x)=ex在x=a時的函式值相同。
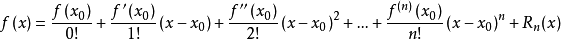
 泰勒公式
泰勒公式

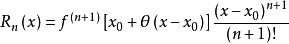


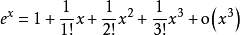
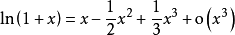
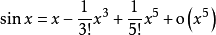
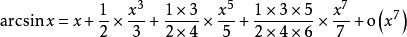
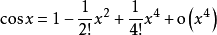

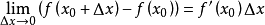

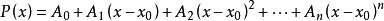

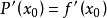
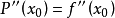




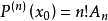
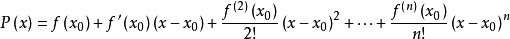
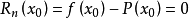
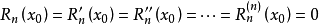
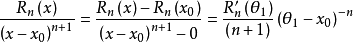



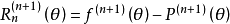
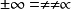
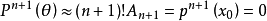
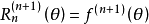
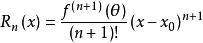
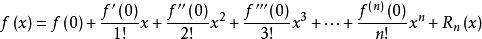
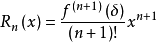

 近似表達正弦函式
近似表達正弦函式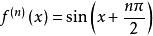


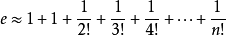
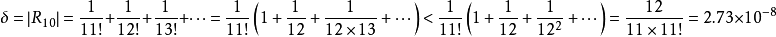
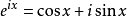
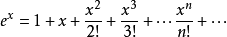
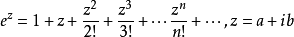
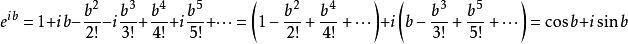
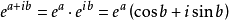
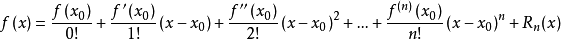
 泰勒公式
泰勒公式

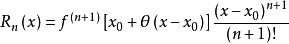


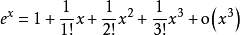
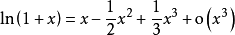
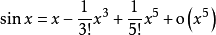
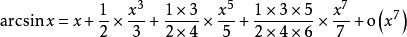
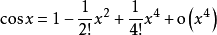
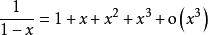

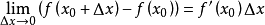

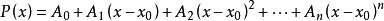

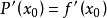
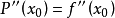




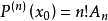
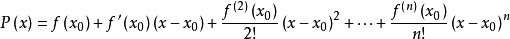
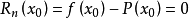
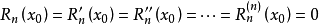
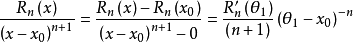



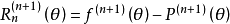
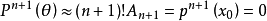
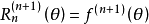
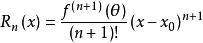
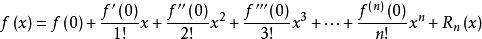
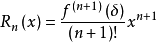

 近似表達正弦函式
近似表達正弦函式