兩個n階拉丁方在同一位置上的數依次配置成對時,如果這兩個有序數對恰好各不相同(一般處理方法為把當中某些行或列對調)(這種相同即經過有限次旋轉和鏡像對稱後不重合)。下面是兩個互為正交的4階拉丁方。
基本介紹
- 中文名:正交拉丁方
- 外文名:orthogonal Latin squares
- 套用領域:正交實驗設計
- 優點:提高實驗的準確度
- 學科:數理科學
類型









套用
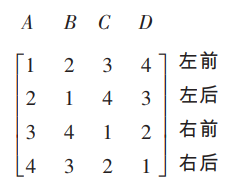 圖1
圖1 圖2
圖2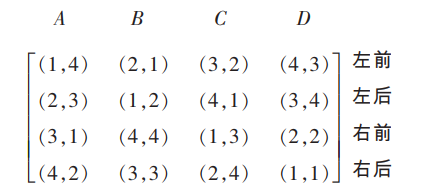 圖3
圖3相關定理


兩個n階拉丁方在同一位置上的數依次配置成對時,如果這兩個有序數對恰好各不相同(一般處理方法為把當中某些行或列對調)(這種相同即經過有限次旋轉和鏡像對稱後不重合)。下面是兩個互為正交的4階拉丁方。









 圖1
圖1 圖2
圖2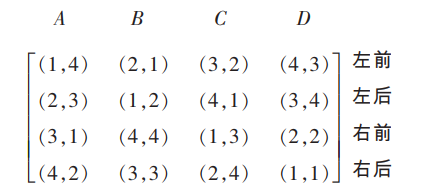 圖3
圖3
兩個n階拉丁方在同一位置上的數依次配置成對時,如果這兩個有序數對恰好各不相同(一般處理方法為把當中某些行或列對調)(這種相同即經過有限次旋轉和鏡像對稱後...
即為一對正交拉丁方。 而在階數固定的情況下,所有兩兩正交的拉丁方所成的集合稱為正交拉丁方族。拉丁方陣構造 請你造一個n=4的正交拉丁方陣。如果...
正交拉丁方設計是使用正交拉丁方安排的一種試驗方案,當存在m個相互正交的n階拉丁方時,用拉丁方的行和列分別表示兩個因素的n個水平,用這m個拉丁方的記號分別表示...
自正交拉丁方(self-orthogonal Latin square)是一類特殊的拉丁方,指與自身的轉置相正交的拉丁方,亦即(2,1,3)共軛正交拉丁方。v階自正交拉丁方存在的充分必要條件...
正交對稱拉丁方是一類組合對象,與羅姆方等價。值得注意的是正交對稱拉丁方不同於通常的正交拉丁方。若t個n階冪等對稱拉丁方中每兩個構成正交對稱拉丁方,則稱它們...
正交拉丁方完備組(complete set of MOLS)一組特殊的正交拉丁方.指v-1個相互正交的v階拉T方.若X=UF
超希臘-拉丁方,即拉丁方陣(英語:Latin square),是一種 n × n 的方陣,在這種 n × n 的方陣里,恰有 n 種不同的元素,每一種不同的元素在同一行或同一...
的存在性則等價於 k-2 個 v 階相互正交拉丁方的存在性。[2] 參考資料 1. 李和平.精細化工工藝學:科學出版社,2005年 2. 《數學辭海》總編輯委員會.《數學...
(v,k;λ),當λ=1時簡記為OA(v,k).OA(v,k;λ)的存在性等價於橫截設計TDλ[k;v]的存在性,OA(v,k)的存在性則等價於k-2個v階相互正交拉丁方的存在...
正交對稱拉T方是一類組合對象...... 對稱拉丁方,若當1Oi<jy時,所有的序對((l;i o m}i)兩兩相異,則稱L與M構成正交對稱拉丁方.值得注意的是正交對稱拉丁...
5.2拉丁方與正交的拉丁方2045.2.1問題的引入2045.2.2正交拉丁方及其性質2055.3域的概念2065.4Galois域GF(pn)2085.5正交拉丁方的構造211...
但到1960年,數學家們徹底解決了這個問題,證明了n=4t+2(t≥2)階歐拉方都是存在的。三十六軍官問題套用 編輯 這種方陣在近代組合數學中稱為正交拉丁方,它在工...
8.2.3正交拉丁方套用舉例 1458.3平衡不完全區組設計 1478.3.1基本概念 1478.3.2關聯矩陣及其性質 1488.3.3三連繫 1528.4幾何設計 154...
6.6 白正交拉丁方6.7 註記第7章 PBD設計的存在性與構作7.1 直接構作法7.2 設計的遞歸構作7.3 PBS閉集的有限生成集與基...
10.4.2 用有限域構造正交拉丁方完備組10.5 Hadamard矩陣10.6 用有限域構造Hadamard矩陣參考資料 1. 組合數學引論 .豆瓣[引用日期2017-09-23] ...
先後主持過河南省科委項目“框架結構的自正交拉丁方的存在性”等。合作主編了由中國科學技術出版社出版的《統計學》一書。1996年以第一完成者獲河南省自然科學優秀...
)。利用有限域的性質可以構造出各種對稱性質的組合結構,如正交拉丁方,平衡區組設計等,這些組合結構有效地套用於試驗設計,通信系統等許多實際領域中,特別隨著計算機技術...
橫截設計是一類特殊的可分組設計。即組的大小全相等且組的個數與區組大小相同的可分組設計。橫截設計的遞推構造方法為正交拉丁方的構造提供了有力的工具。橫截...
正交拉丁方及其套用 杜北梁 1997年獲江蘇省科技進步三等獎 連續鑄鋼二冷傳熱模型的計算軟體 岳興業、易法槐 1996年獲江蘇省科技進步四等獎 g-函式與k-網 惲...
10.2 平衡不完全區組設計 10.3 幾何設計 10.4 正交拉丁方 10.5 Hadamard矩陣 10.6 用有限域構造Hadamard矩陣 [1] 參考資料 1. . ..[引用日期2016-03-...
3.布局,包括正交拉丁方、區組設計、正交表、阿達馬矩陣、差集等.經典組合學常討論以下三個問題,即特定安排的存在性問題、特定安排的計數間題和尋求在某個最佳化準則...
附表5平衡不完全區組設計表 附表6正交拉丁方表 附表7正交表 附表8正交表構造的運算法則 附表9百分率換算為角度值表 主要參考文獻參考...
平面設計與正交拉丁方 17.4 有限射影空間與區組設計 17.5 有限向量空間與區組設計第十八章 完全設計和正交設計 18.1 拉丁方 18.2 完備拉丁方 18.3 正交侶...
研究方向為組合數學,主要從事組合設計及其在密碼上套用的研究工作,以區組設計、正交拉丁方、圖分解、擬群以及信息認證和密鑰管理的組合結構為主要研究對象. 所研究的...
