性質
(以下性質所用符號均如圖1所示)
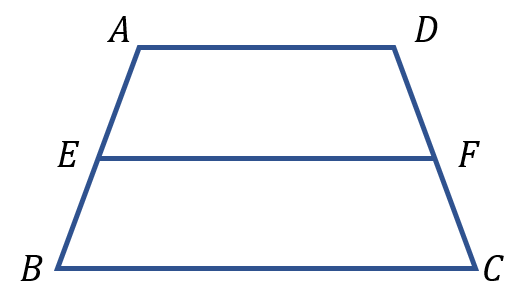 圖1 梯形示例
圖1 梯形示例2、梯形的中位線(
),平行於兩底並且等於上下底和的一半
。
判定
1、一組對邊平行,另一組對邊不平行的四邊形是梯形。
2、一組對邊平行且不相等的四邊形是梯形。
特殊梯形
等腰梯形
定義
兩腰相等的梯形叫做
等腰梯形(isosceles trapezoid)
性質
1、等腰梯形的兩條腰相等。
2、等腰梯形在同一底上的兩個底角相等。
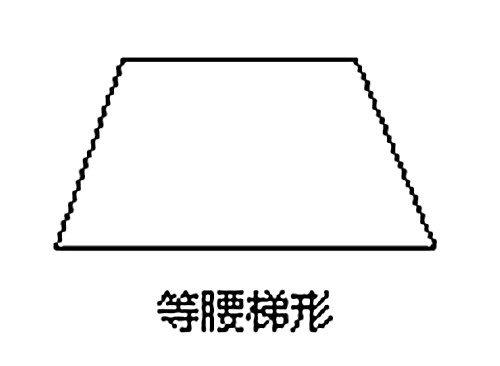 圖2a等腰梯形
圖2a等腰梯形4、等腰梯形是
軸對稱圖形,對稱軸是上下底中點的連線所在直線(過兩底中點的直線)。
判定
1、兩腰相等的梯形是等腰梯形;
2、同一底上的兩個角相等的梯形是等腰梯形;
3、對角線相等的梯形是等腰梯形。
直角梯形
定義
一腰垂直於底的梯形叫
直角梯形(right trapezoid)。
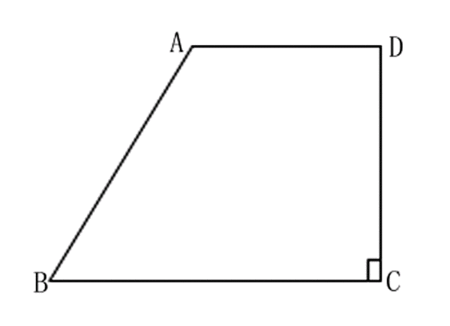 圖2b直角梯形
圖2b直角梯形性質
2、有一定的穩定性,但弱於非直角梯形。
判定
1、一腰垂直於底的梯形是直角梯形;
2、有一個內角是直角的梯形是直角梯形。
周長與面積
周長
梯形的周長公式:設梯形的上底長為
,下底長為
,兩腰長分別為
、
,周長為
,則梯形的周長公式為
通俗表示為:上底+下底+腰+腰
等腰梯形的周長公式:由於等腰梯形的兩腰長相等,即
,故等腰梯形的周長公式可簡化為
通俗表示為:上底+下底+2腰
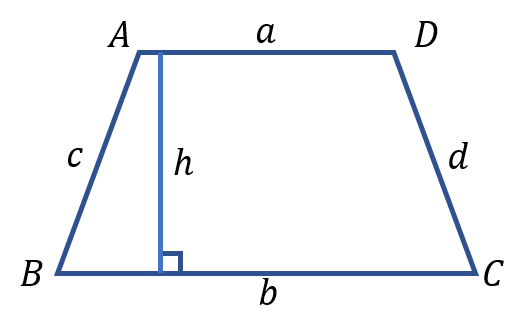 圖3梯形的周長與面積
圖3梯形的周長與面積面積
梯形的面積公式:設梯形的上底長為
,下底長為
,高為
,面積為
,則梯形的面積公式為
通俗表示為:(上底+下底)×高÷2
特例:
1、若已知梯形中位線長度為
,根據上述梯形性質2,則梯形面積公式為
2、若梯形的兩條對角線相互垂直,長度分別為
、
,則梯形面積公式為
。
3、若梯形的底和腰的長度已知、高的長度未知,則梯形面積公式為
常用輔助線
1、作高(根據實際題目確定);
2、平移一腰;
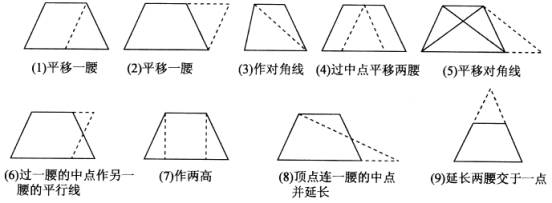 圖4 常用輔助線做法
圖4 常用輔助線做法4、反向延長兩腰交於一點;
5、取一腰中點,另一腰兩端點連線並延長;
7、 取兩腰中點,連線,作中位線 。
經典例題
例 1
如圖5,△ABC中,AB=AC,BD、CE分別為∠ABC、∠ACB的平分線。求證:四邊形EBCD是等腰梯形。
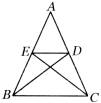 圖5 例1
圖5 例1分析:欲證四邊形EBCD是等腰梯形,解題思路是證ED//BC,BE=CD,由已知條件易證△BCD≌△CBE得到EB=DC,從而AE=AD,運用等腰三角形的性質可證ED//BC。
證明:
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DBC=∠ECB=1/2∠ABC,
∴△EBC≌△DCB(A。S。A),
∴BE=CD,
∴AB-BE=AC-CD,即AE=AD.
∴∠ABC=∠AED,∴ED//BC,
又∵EB與DC交於點A,即EB與DC不平行,
∴四邊形EBCD是梯形,又BE=DC,
∴四邊形EBCD是等腰梯形.
提示:本題的解題關鍵是證明ED//BC,EB=DC,易錯點是忽視證明EB與DC不平行。
例 2
如圖6,已知四邊形ABCD中,AB=DC,AC=DB,求證:四邊形ABCD是等腰梯形。
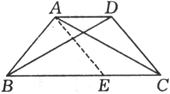 圖6 例2
圖6 例2證明:
過點A作AE∥DC交BC邊於點E.
∵AB=CD,AC=DB,
∴△ABC≌△DCB,∴∠ABC=∠DCB
又∵AE∥DC,
∴∠AEB=∠DCB
∴∠ABC=∠AEB ,∴AB=AE,
∴四邊形AECD是平行四邊形.
∴AD∥BC.
又AB=DC,且AD≠BC,
∴四邊形ABCD為等腰梯形.
提示:判定一個任意四邊形為等腰梯形,如果不能直接運用等腰梯形的判定定理,一般的方法是通過作輔助線,將此四邊形分解為熟悉的多邊形,此例就是通過作平行線,將四邊形分解成為一個平行四邊形和一個等腰三角形。
例 3
如圖7,P為等腰梯形ABCD的下底BC上一點,PM⊥AB,PN⊥CD,M,N為垂足,BE⊥CD,E為垂足.求證:BE=PM+PN.
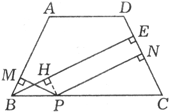 圖7 例3
圖7 例3證明:
過P點作PH⊥BE於點H.
∵BE⊥CD,PN⊥CD,
∴四邊形PHEN是矩形.
∴HE=PN,EN∥PH.
∴∠BPH=∠C.
∵四邊形ABCD為等腰梯形,
∴∠ABC=∠C.
∴∠MBP=∠HPB.
又∵PM⊥AB,BP公共,
∴Rt△MBP≌Rt△HPB.
∴PM=BH.
∴BE=BH+HE=PM+PN.
提示:要證線段的和差問題,通常可以考慮用“截長法”或“補短法”來完成,本例採用的是“截長法”。
例 4
如圖8,在梯形ABCD中,AD∥BC,且AB=AD+BC,M為DC的中點.求證:AM⊥BM。
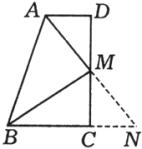 圖8 例4
圖8 例4證明:
延長AM交BC的延長線於點N.∵M為DC中點,AD∥BC,
∴△ADM≌△NCM.
∴AD=CN,AM=MN.
∴AB=AD+BC=BN.
提示:根據證題的需要,集中梯形的兩底也是常用的添加輔助線的方法.本例也可以先延長BC至N,使BN=AB,再證A、M、N共線。
例 5
如圖9,梯形ABCD中,AD∥BC,對角線AC⊥BD,且AC=5cm,BD=12cm,求該梯形上下底的和.
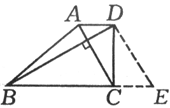 圖9
圖9解:
過D作DE∥AC交BC的延長線於點E.
∵AD∥CE,∴DE=AC=5cm,AD=CE.
∵AC⊥BD,
∴DE⊥BD.
在Rt△BDE中,
∴AD+BC=CE+BC=BE=13cm.
提示:過頂點作一條對角線的平行線,把兩條對角線的數量關係和位置關係集中到一個三角形中,將求梯形上下底的長轉化為求直角三角形斜邊的長。
例 6
如圖10,在等腰梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AF是梯形的高,梯形的面積是49cm2.求梯形的高。
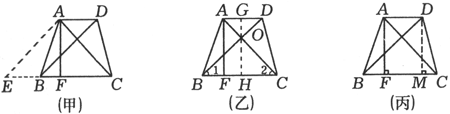 圖10 例6
圖10 例6解法1:
如圖10(甲),過A作AE∥DB交CB的延長線於點E。
∵AC⊥BD,
∴AC⊥AE.
∵AD∥EB,
∴AE=BD,EB=AD.
又∵四邊形ABCD是等腰梯形,
∴AC=BD.
∴AE=AC.
∴△AEC是等腰直角三角形.
又AF是斜邊上的高,故AF也為斜邊上的中線.
∴AF=7cm
解法2:
設梯形ABCD的兩條對角線相交於O點,過O作OH⊥BC於點H,延長HO交AD於G點(如圖10(乙)).
∵AD∥BC,
∴HG⊥AD.
∵AB=DC,AC=DB,BC公共,
∴△ABC≌△DCB.
∴∠2=∠1.
又∵AC⊥BD,
∴△BOC是等腰直角三角形。
∴同理.
∴以下解答過程與解法1相同。
解法3:
過D作DM⊥BC於點M(如圖10(丙)).
∵梯形ABCD是等腰梯形,
∴AC=DB,∠ABC=∠DCB.
又∵AF=DM,
∴Rt△AFC≌Rt△DMB,
∴∠DBC=∠ACB.
又∵AC⊥BD,
∴∠DBM=∠ACF=45°.
∴△AFC和△DMB都是等腰直角三角形.AF=FC,DM=MB,
∴以下解答過程與解法1相同.
提示:本題的三種解法都是利用等腰直角三角形的性質或全等三角形的性質來證明該梯形的高就等於該梯形的中位線的長.因此,在等腰梯形中,若兩條對角線垂直,則這個梯形的高就等於中位線的長,梯形的面積就等於高的平方。
例 7
如圖11,在梯形ABCD中,AD//BC,AB=DC,點E,F,G分別在邊AB,BC,CD上,且AE=GF=GC.
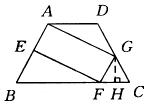 圖11 例7
圖11 例7(1)求證四邊形AEFG是平行四邊形;
(2)當∠FGC=2∠EFB時,求證四邊形AEFG是矩形.
分析:本題考查有關三角形、四邊形的綜合證明.涉及到等腰梯形的性質、平行四邊形的判定與性質、等腰三角形的性質等.在解答過程中要注意證明格式、推理方式的規範化.
證明:
(1)∵在梯形ABCD中,AB=DC,
∴∠B=∠C.
∵GF=GC,∴∠C=∠GFC,
∴∠B=∠GFC
∴AB//GF,即AE//GF.
又∵AE=GF
∴四邊形AEFG是平行四邊形.
(2)解:過點G作GH⊥FC,垂足為H.
∵GF=GC,
∴∠FGH=1/2∠FGC.
∵∠FGC=2∠EFB
∴∠FGH=∠EFB.
∵∠FGH+∠GFH=90°
∴∠EFB+∠GFH=90°
∴∠EFG=90°
∵四邊形AEFG是平行四邊形,
∴四邊形AEFG是矩形.
備註:梯形的底角可以指梯形中任意一個角,所以說“底角相等的梯形是等腰梯形”是不對的。
 圖1 梯形示例
圖1 梯形示例


 圖2a等腰梯形
圖2a等腰梯形 圖2b直角梯形
圖2b直角梯形


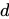



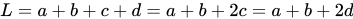
 圖3梯形的周長與面積
圖3梯形的周長與面積




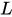
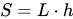
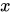

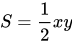
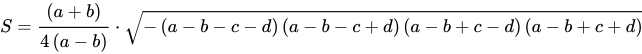
 圖4 常用輔助線做法
圖4 常用輔助線做法 圖5 例1
圖5 例1 圖6 例2
圖6 例2 圖7 例3
圖7 例3 圖8 例4
圖8 例4 圖9
圖9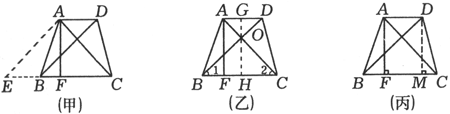 圖10 例6
圖10 例6 圖11 例7
圖11 例7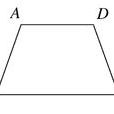
 圖1 梯形示例
圖1 梯形示例


 圖2a等腰梯形
圖2a等腰梯形 圖2b直角梯形
圖2b直角梯形


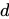



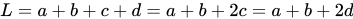
 圖3梯形的周長與面積
圖3梯形的周長與面積




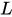
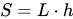
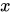

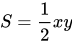
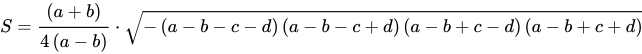
 圖4 常用輔助線做法
圖4 常用輔助線做法 圖5 例1
圖5 例1 圖6 例2
圖6 例2 圖7 例3
圖7 例3 圖8 例4
圖8 例4 圖9
圖9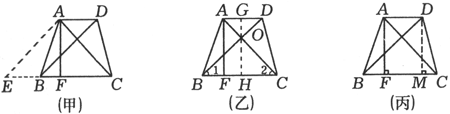 圖10 例6
圖10 例6 圖11 例7
圖11 例7