基本介紹
- 中文名:柯爾莫哥洛夫強大數律
- 外文名:Kolmogorov strong law of large numbers
- 所屬學科:數學
- 所屬問題:機率論(大數律)
- 提出者:柯爾莫哥洛夫
基本介紹




















兩種情形







大數律


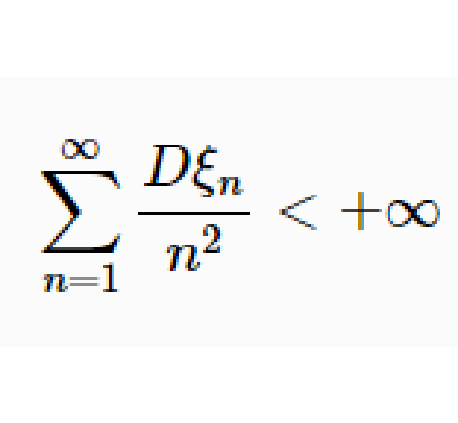





























柯爾莫哥洛夫強大數律(Kolmogorov strong law of large numbers)是最重要最常用的強大數律。若{Xn}為獨立同分布隨機變數序列,EXn存在,則以機率1成立n個獨立同...
強大數定律主要包括波萊爾強大數定律、柯爾莫哥洛夫強大數定律等。 強大數定律首先由法國數學家Borel對於伯努利隨機變數的特殊情況進行證明,一般情形下的強大數定律的...
柯爾莫哥洛夫,為機率論建立了公理體系的蘇聯數學家。...... 柯爾莫哥洛夫,為機率論建立了公理體系的蘇聯數學...20年代關於強大數律、重對數律的基本工作;1933年...
德雷·柯爾莫哥洛夫(俄語:Андре́й Никола́евичКолмого́ров,1903年4月25日-1987年10月20日),俄國數學家,主要在...
安德列·柯爾莫哥洛夫(1903年4月25日-1987年10月20日),20世紀蘇聯最傑出的數學家,也是20世紀世界上為數極少的幾個最有影響的數學家之一。他的研究幾乎遍及...
安德列·柯爾莫哥洛夫(1903年4月25日-1987年10月20日),20世紀蘇聯最傑出的數學家,也是20世紀世界上為數極少的幾個最有影響的數學家之一。他的研究幾乎遍及...
獨立隨機變數序列是機率論的重要領域,他首先與A.H.柯爾莫哥洛夫討論了隨機變數級數的收斂性。他證明了:①作為強大數律先聲的辛欽弱大數律;②隨機變數的無窮小三...
1933年蘇聯的柯爾莫哥洛夫提出機率論的公理化體系,提出並完成了著名的強大數定理的推論。公理化體系標誌著機率論已成為一門成熟的數學學科,同時也是近代機率論的...
1931年,安德雷·柯爾莫哥洛夫(АндрейНиколаевичКолм...遍歷定理的證明依賴於強大數定律(Strong Law of Large Numbers, SLLN),表明...
他首先與柯爾莫哥洛夫討論了隨機變數級數的收斂性,他證明了:(1)作為強大數律先聲的辛欽弱大數律;(2)隨機變數的無窮小三角列的極限分布類與無窮可分分布類相同...
1933年蘇聯的柯爾莫哥洛夫提出機率論的公理化體系,提出並完成了著名的強大數定理的推論。公理化體系標誌著機率論已成為一門成熟的數學學科,同時也是近代機率論的...
一個隨機過程的機率分布律可由規定它的隨機變數的有限維聯合分布給出。根據其中...1933年蘇聯的柯爾莫哥洛夫提出機率論的公理化體系,提出並完成了著名的強大數...
1949年 J.L.杜布指出柯爾莫哥洛夫-斯米爾諾夫統計量的極限分布與布朗橋的上...從強大數律到重對數律也是一種精確化,而強不變原理起到了類似的作用。...
§4.2大數律和強大數律 §4.3中心極限定理 §4.4補充知識 習題四 第五...附表5柯爾莫哥洛夫檢驗的臨界值表 參考文獻 名詞索引北京大學數學教學系列叢書...
