基本介紹
- 中文名：拓補學
- 外文名：Topology
- 類別：數學分支
- 分類：點集拓補學、代數拓補學等
概述,分支學科,拓補問題,紐結問題,
概述
數學中一個重要的、基礎的分支。起初它是幾何學的一支,研究幾何圖形在連續變形下保持不變的性質(所謂連續變形，形象地說就是允許伸縮和扭曲等變形，但不許割斷和粘合);現在已發展成為研究連續性現象的數學分支。由於連續性在數學中的表現方式與研究方法的多樣性，拓撲學又分成研究對象與方法各異的若干分支.在拓撲學的孕育階段，19世紀末，就已出現點集拓撲學與組合拓撲學兩個方向。現在前者已演化成一般拓撲學，後者則成為代數拓撲學。後來，又相繼出現了微分拓撲學、幾何拓撲學等分支。拓撲學主要是由於分析學和幾何學的需要而發展起來的,它自30年代以來的大發展,尤其是它的成果與方法對於數學的各個領域的不斷滲透，是20世紀理論數學發展中的一個明顯特徵。
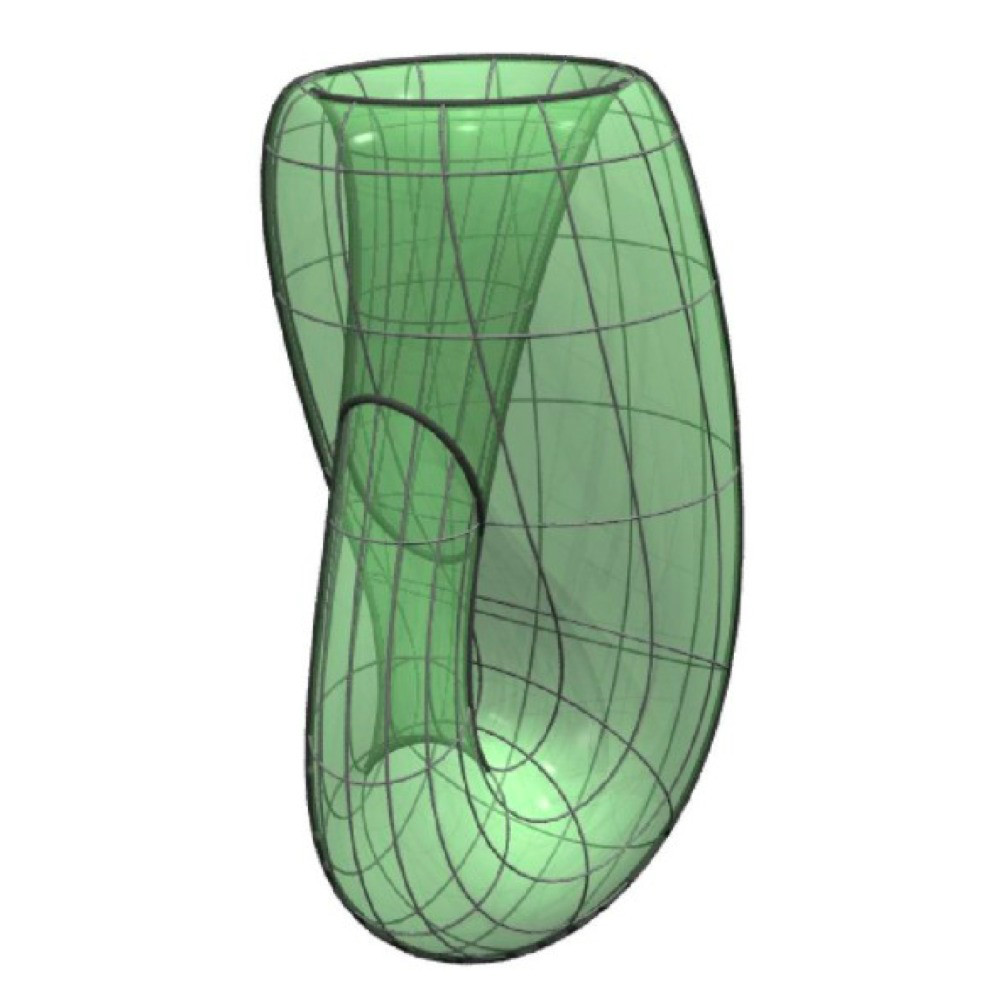
上下對摺再左右對摺形成輪胎形狀圖A分支學科
點集拓補學又稱為一般拓補學
代數拓補學
微分拓補學
幾何拓補學
拓補學的主要套用是在分子生物學中。當談到脫氧核糖核酸的三級結構，就必然會談到所謂的“超螺旋結構”。這種超螺旋結構可以解釋為：發生螺旋纏繞的螺旋結構，換句話說，就是一個螺旋結構再一次進行螺旋纏繞。脫氧核糖核酸原本就是雙股螺旋，而這雙股螺旋又會再進一步進行螺旋纏繞，形成所謂的超螺旋結構。
拓補學就是用來研究超螺旋結構的一種工具。拓補學主要探討的是在連續性變化中（比如因為溫度改變而發生構型改變時，或因為與蛋白質作用而發生互動作用時）的變形現象。拓補性質不包含非連續性變化時產生的變形作用（雙股螺旋被剪開時的狀況）。對於去氧核糖核酸而言，那些當沒有打斷股鏈時，不受變形現象而改變的性質就叫拓補性質。拓補性質的改變只受到打斷股鏈或將股鏈粘合的影響。
拓補問題
拓撲問題的一些初等例子（右圖上下左右對摺以後就是一個輪胎形狀，有7個區域兩兩相連。國外數學家給出）
柯尼斯堡的七橋問題（一筆畫問題） 柯尼斯堡是東普魯士首府，普萊格爾河橫貫其中，上有七座橋（見圖論）。一個散步者怎樣才能走遍七座橋而每座橋只經過一次？這個18世紀的智力遊戲，被L.歐拉簡化為用細線畫出的網路能否一筆畫出的問題，然後他證明這是根本辦不到的。一個網路之能否一筆畫出，與線條的長短曲直無關，只決定於其中的點與線的連線方式。構想一個網路是用柔軟而有彈性的材料製作的，在它被彎曲、拉伸後，能否一筆畫出的性質是不會改變的。歐拉的多面體公式與曲面的分類 歐拉發現，不論什麼形狀的凸多面體，其頂點數V、棱數 E、面數F之間總有:V-E+F=2這個關係。從這個公式可以證明正多面體只有五種（見正多面體）。值得注意的是，如果多面體不是凸的而呈框形（圖1凸形與框形）,也不管框的形狀如何，總有□。這說明，凸形與框形之間有比長短曲直更本質的差別，通俗的說法是框形里有個洞。 連續變形下，凸體的表面可以變為球面，框的表面可以變為環面（輪胎面）。這兩者卻不能通過連續變形互變。在連續變形下封閉曲面有多少種不同類型？怎樣鑑別它們？這曾是19世紀後半葉拓撲學研究的主要問題。把曲面變形成多面體後的歐拉數□-□+□在其中起著關鍵的作用（見閉曲面的分類）。四色問題 在平面或球面上繪製地圖，有公共邊界線的區域用不同的顏色加以區別。19世紀中期，人們從經驗猜想用四種顏色就足以給所有的地圖上色。證明這個猜想的嘗試，卻延續了100多年,到1976年才出現了一個藉助於計算機的證明。如果不是在平面上而是在輪胎面上畫地圖，四色就不夠了，要七色才夠。用橡皮做一個曲面模型，然後隨意扭曲，弄得山巒起伏，這對其上的地圖著色毫無影響，所以這顏色數也是曲面在連續變形下不變的性質。右圖是一個有2個洞的曲面，需要8種顏色（8個區域兩兩相連，王曉明王蕊珂用了9年給出）。
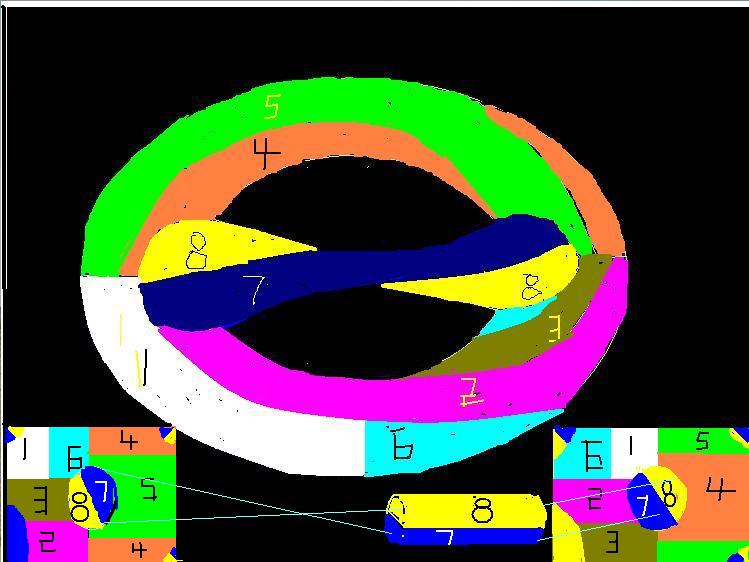虧格為2時8個兩兩相連區域紐結問題
空間中一條自身不相交的封閉曲線，會發生打結現象。要問一個結能否解開（即能否變形成平放的圓圈）,或者問兩個結能否互變（例如，圖2圓圈與三葉結中的兩個三葉結能否互變），並且不只做個模型試試，還要給出證明，那就遠不是件容易的事了（見紐結理論）。
維數問題 什麼是曲線？樸素的觀念是點動成線，隨一個參數（時間）連續變化的動點所描出的軌跡就是曲線。可是，G.皮亞諾在1890年竟造出一條這樣的“曲線”，它填滿整個正方形！這激發了關於維數概念的深入探討，經過20～30年才取得關鍵性的突破（見維數）。 布線問題（嵌入問題） 一個複雜的網路能否布在平面上而不自相交叉？做印刷電路時自然會碰到這個問題。圖3可嵌入網路中左面的圖把一根對角線移到方形外面就可以布在平面上,但圖4不可嵌入網路兩個圖卻無論怎樣挪動都不能布在平面上。1930年K.庫拉托夫斯基證明，一個網路是否能嵌入平面，就看其中是否不含有這兩個圖之一。 向量場問題 考慮光滑曲面上的連續的切向量場，即在曲面的每一點放一個與曲面相切的向量，並且其分布是連續的。其中向量等於0的地方叫作奇點。例如,地球表面上每點的風速向量就組成一個隨時間變化的切向量場,而奇點就是當時沒風的地方。從直觀經驗看出,球面上的連續切向量場一定有奇點，而環面上卻可以造出沒有奇點的向量場。
進一步分析，每個奇點有一個“指數”，即當動點繞它一周時,動點處的向量轉的圈數；此指數有正負,視動點繞行方向與向量轉動方向相同或相反而定(圖5向量場齊點的指數)。龐加萊發現，球面上切向量場,只要奇點個數是有限的，這些奇點的指數的代數和（正負要相消）恆等於2；而環面上的則恆等於0（見曲面）。這2與0恰是那兩個曲面的歐拉數，這不是偶然的巧合。
不動點問題 考慮一個曲面到自身的連續變換（映射）,即曲面的每一點被移到該曲面上。右圖，上面圖，上下對摺再左右對摺，形成一個輪胎形狀，再把下面的四叉按照ABCD安裝在輪胎上，就是一個有4個洞的10個區域兩兩相連。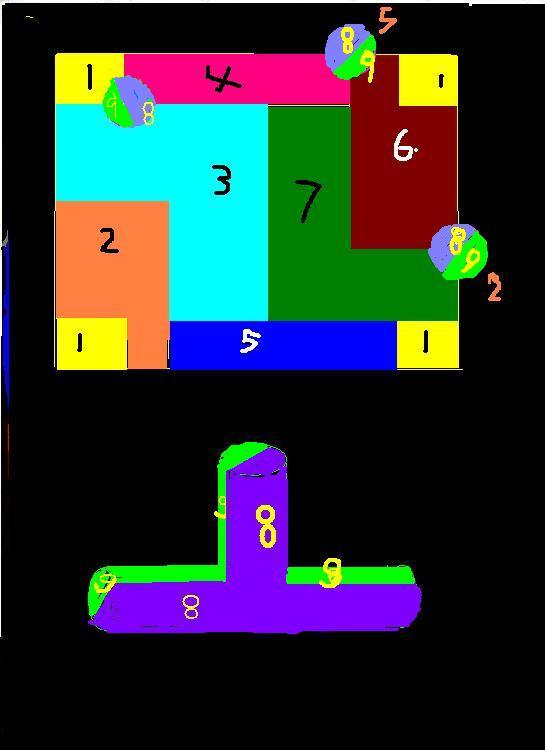
虧格3時9個區域兩兩相連
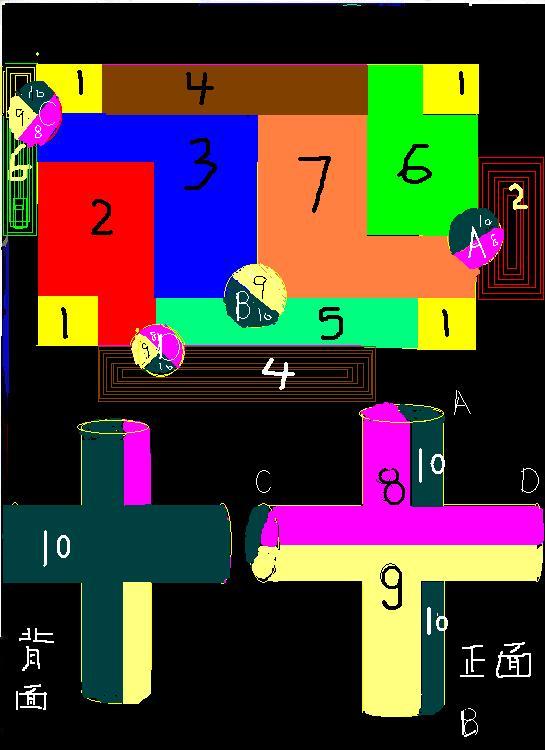虧格為4時9個區域兩兩相連
虧格3時9個區域兩兩相連虧格為4時9個區域兩兩相連