平面鑲嵌

基本概念 用若干類全等形（能夠完全重合的圖形叫做全等形）無間隙且不重疊地覆蓋平面的一部分，叫做這幾類圖形能鑲嵌（覆蓋、鋪砌）平面．鑲嵌的一個關鍵點是：在每個公共頂點處，各角的和是360°．最簡單的鑲嵌是只用一類全等形鑲嵌平面．以下對平面鑲嵌問題從三個方面略作介紹．

另外，平面鑲嵌又稱為“平面密鋪”。平面鑲嵌的條件：不重疊，無縫隙。

基本介紹

• 中文名：平面鑲嵌
• 又稱：“平面密鋪”
• 條件：不重疊，無縫隙
• 關鍵點：在每個公共頂點處各角的和是360°

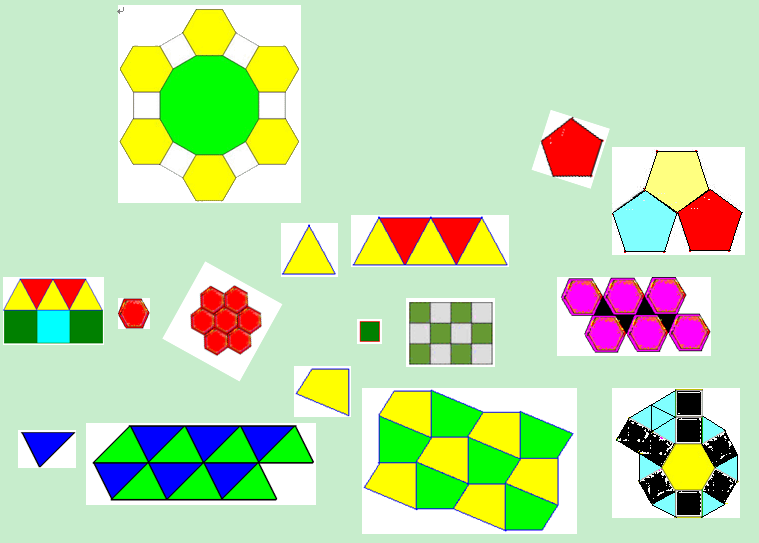
三個方面

用一種任意多邊形鑲嵌

1．全等的任意三角形能鑲嵌平面

把一些紙整齊地疊放好，用剪刀一次即可剪出多個全等的三角形．用這些全等的三角形可鑲嵌平面．這是因為三角形的內角和是180°，用6個全等的三角形即可鑲嵌出一個平面．如圖1．

用全等的三角形鑲嵌平面，鑲嵌的方法不止一種，如圖2．

2．全等的任意四邊形能鑲嵌平面。

仿上面的方法可剪出多個全等的四邊形，用它們可鑲嵌平面．這是因為四邊形的內角和是360°，用4個全等的四邊形即可鑲嵌出一個平面．如圖3．其實四邊形的平面鑲嵌可看成是用兩類全等的三角形進行鑲嵌．如圖4．

3．全等的特殊五邊形可鑲嵌平面

聖地亞歌一位家庭婦女，五個孩子的母親瑪喬里·賴斯，對平面鑲嵌有很深的研究，尤其對五邊形的鑲嵌提出了很多前所未有的結論．1968年克什納斷言只有8類五邊形能鑲嵌平面，可是瑪喬里·賴斯後來又找到了5類五邊形能鑲嵌平面，在圖5的五邊形ABCDE中，∠B=∠E=90°，2∠A+∠D=2∠C+∠D=360°，a=e，a+e=d．圖6是她於1977年12月找到的一種用此五邊形鑲嵌的方法．用五邊形鑲嵌平面，是否只有13類，還有待研究．

4．全等的特殊六邊形可鑲嵌平面

1918年，萊因哈特證明了只有3類六邊形能鑲嵌平面．圖7是其中之一．在圖7的六邊形ABCDEF中，∠A+∠B+∠C=360°，a=d．

5．七邊形或多於七邊的凸多邊形，不能鑲嵌平面．

用同一種正多邊形鑲嵌

只有正三角形、正方形和正六邊形可鑲嵌平面，用其它正多邊形不能鑲嵌平面．

用多種正多邊形鑲嵌

所有的方法：
用1種：（3，3，3，3，3，3）（4，4，4，4）（6，6，6）；
用2種：（4，8，8）（3，12，12）（3，3，6，6）（3，3，3，3，6）（3，3，3，4，4）（5，5，10）
用3種：（3，4，4，6）（4，6，12）（3，3，4，12）（3，10，15）（3，9，18）（3，8，24）（3，7，42）（*4，5，20）
其中的數字分別代表正多邊形的邊數。共有17種。
是枚舉出來的。
證明不能用3種以上的多邊形鑲嵌：
因為若用4種，則內角和最小為60+90+108+120=378>360，（三角形、正方形、正五邊形、正六邊形）。
另外其中帶星號的的兩個（5,10,10）（3,7,42）是只能在一個點鑲嵌，而不能在整個平面鑲嵌。不帶這兩個，則是有15種方法。

例如：用正三角形和正六形的組合進行鑲嵌．設在一個頂點周圍有m個正三角形的角，有n個正六邊形的角．由於正三角形的每個角是60°，正六邊形的每個角是120°．所以有

m·60°+n·120°=360°，即m+2n=6．

這個方程的正整數解或可見用正三角形和正六邊形鑲嵌，有兩種類型，一種是在一個頂點的周圍有4個正三角形和1個正六邊形，另一種是在一個頂點的周圍有2個正三角形和2個正六邊形．如圖8、圖9．

教學流程

教學課堂教學的流程可以大致如下：

課前師生收集鑲嵌圖案——課堂展示交流有關鑲嵌圖案——明晰概念（鑲嵌）——對所展示圖片觀察的基礎上提出一些有待研究的問題——對學生所提出問題進行適當的歸類並進一步引導以展開後續的課堂教學。

學生所提出的問題必將是十分豐富的，同時也可能是十分繁雜的。因此，教師課前應認真分析有關問題，根據學生的學習經驗、思維水平以及問題之間的邏輯關係對後續問題的研究進行一個整體的規劃，這樣才能及時對學生所提出的問題有一個比較好的評判（如對這個問題的研究價值、研究方法、研究難度等作出比較恰當的評判，從而確定這樣的問題是否可以在課堂上進行研究，按照什麼順序進行研究等），從而保證課堂教學的有序而高效地進行。固然，教學中可以有多樣的選擇，下面僅提出一些建議供參考。

總體而言，教學中應認真分析問題的繁簡和難易程度，一般遵循先易後難、先簡後繁的順序展開教學活動。因此，建議首先研究較為簡單的單個多邊形的鑲嵌問題，再研究複雜的多個多邊形的組合鑲嵌問題。

對於單個多邊形的鑲嵌問題，基於學生的水平和課程標準的要求，這裡主要研究三角形、四邊形、正六邊形的鑲嵌問題。

對於三角形、正六邊形以及一些特殊的四邊形（如正方形、長方形、平行四邊形）的鑲嵌問題，學生應該都比較熟悉，因此，教學中，教師可以根據課堂教學狀況靈活選擇不同的教學順序。如可以在收集、觀察的基礎上發現正方形、正六邊形等平面圖形都可以鑲嵌整個平面，然後思考還有哪些正多邊形也可以鑲嵌整個平面，再從特殊到一般進一步研究一般的多邊形（三角形、四邊形）的鑲嵌問題；也可以在明晰了鑲嵌概念之後，直接要求學生想像哪些多邊形能夠鑲嵌平面，並進行具體的紙上描畫或者進行實際的拼接（當然，這裡就未必有一個確定的教學順序了，根據課堂學生的狀況可能有不同的教學順序）。顯然，對於前一種處理方式，課堂教學的邏輯順序更為明顯，教學易於操控；而對於後一種處理方式，給學生和教師都留下了比較大的空間，教學將更為開放，課堂更具生成性，但同時也不可避免具有一定的不可操控性，對教師自身素質提出了更高的要求。

一般四邊形的鑲嵌問題，是這堂課地教學難點。如何突破，這是擺在老師們面前的一個課題。這裡可以有多種方式：如，考慮到該鑲嵌圖案的探究對學生而言確實有難度，可以在學生一定的拼接活動的基礎上“告訴”，或者藉助現實生活中一些具體圖形（如一些道路護坡的圖片）直接“告訴”；也可以引導學生關注三角形、平行四邊形等不同的鑲嵌圖案之間的關係以及同一個鑲嵌圖案中各個多邊形之間的變換關係，然後通過適當的變式揭示四邊形的鑲嵌問題（見參考案例）。在獲得一般四邊形的鑲嵌圖案（如甲圖）之後，可能學生還有一些疑問，如四邊形所構成的圖案是“凹凸不平”的，如何鋪滿整個平面？為此，可以通過具體的拼接活動讓學生獲得進一步的直觀感受；或者分析共頂點的四個四邊形組成的“基本圖案”（如乙圖），發現將“基本圖案”中的兩個三角形剪下後平移即可得到一個平行四邊形（如丙圖），而平行四邊形是可以鑲嵌整個平面的，因此，這裡“基本圖案”的鑲嵌相當於將平行四邊形中剪下了部分移入另一個臨近的平行四邊形中。這樣，不僅關注了什麼圖形能夠鑲嵌，而且關注了鑲嵌圖形的形成過程，可以為鑲嵌圖形的設計提供一些參考。