基本介紹
- 中文名:局部環
- 外文名:Stellenringe
- 領域:數學
定義
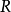


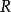




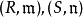

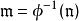
例子





動機與幾何詮釋
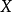



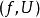




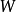





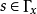


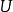







非交換的情形







- R 的唯一極大左理想。
- R 的唯一極大右理想。
- R 的Jacobson根。
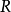


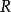




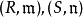

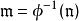





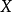



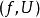




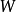





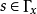


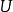














在數學中,局部環是只有一個極大理想的交換含麼環。局部環的概念由 Wolfgang Krull 於1938年引入,稱之為Stellenringe,英譯 local ring 源自扎里斯基。...
電網局部環式運行指電網局部的每一點都能從一個或兩個電源沿兩條不同線路供電的運行方式。如果該電網中每一點正常都由兩條線路供電,則該運行方式稱“閉環”;...
局部代數(local algebra)是與局部環相應的一類特殊代數。菲廷(Fitting,H.)證明了:若A模N的自同態代數EndA(N)是局部的,則N不可分解。當A是域F上有限維代數時...
扎里斯基環是一種特殊的諾特拓撲環。設 (R,m) 是一個諾特局部環,則帶有 m 進拓撲的環 R 是典型的扎里斯基環的例子。...
半完全環是介於完全環與半局部環之間的一類環。設J(R)是環R的雅各布森根,若R/J (R)是半單環,且R/J (R)的冪等元可提升為R的冪等元,則稱R為半完全...
素環是一類重要的環。若環R的零理想是素理想,則稱R為素環。整環、單環、本原環都是素環。素環與素理想有如下關係:P是R的素理想若且唯若R/P是素環。....
環空間((ringed space)一類重要的拓撲空間.指一種帶有一個環層Ox的拓撲空間X.環層Ox被稱為環空間(X,Ox)的結構層一般地,Ox是一個帶單位元的交換環層.環...
諾特概形(Noetherian scheme)是諾特環的推廣。若一個概形X有一個由諾特環的譜所構成的有限仿射開覆蓋,則稱X是諾特概形。概形是代數幾何的基本研究對象。它實際...
概形是代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間。更精確地,概形(X,OX)是一個環空間,其拓撲空間X有一個開覆蓋{Xi}i∈I,...
凡擬優環皆為永田環,所以代數幾何中處理的環幾乎都是永田環。是諾特整環而非永田環的例子首先由秋月康夫於1935年給出。...
概形(scheme)代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間.更精確地,概形(X,Ox)是一個環空間,其拓撲空間X有一個開覆蓋{X,. ...
線上性代數中,迪厄多內行列式是矩陣與除環和局部環上矩陣的行列式的推廣。 它是在1943年由迪厄多內提出的。...
H環(H-ring)概括半局部環與阿廷半單環的一種環類.若環R滿足KZ(R)CH<R),則稱R為H環.這類環對環的直和是封閉的,且H環上的全陣環也是H環.對交換的H...
半素環是一類重要的環。若環 R 的零理想是半素理想,則稱R為半素環。環R是半素的充分必要條件是:R的貝爾根為零,或R無非零的冪零理想。半素環恆為素環的...
在交換代數中,科恩-麥考利環是對應到一類代數幾何性質(例如局部等維性)的交換環。...... 正則局部環皆為Cohen-Macaulay 環。 Gorenstein環皆為 Cohen-Macaulay,其中...
戴德金有限環(Dedekind finite ring)一類特殊環.它的左逆元也是右逆元一個環R,對任意x,yER,若xy=1則yx=1,就稱R為戴德金有限環.例如半局部環、左(右)自...
在抽象代數中,交換代數旨在探討交換環及其理想,以及交換環上的模。代數數論與代數幾何皆奠基於交換代數。交換環中最突出的例子包括多項式環、代數整數環與p進數環,...
6.局部環流和洋流如信風帶大陸西岸,因受離岸風及沿岸寒流的影響,在海岸帶形成沙漠。7.局部地熱異常如在冰島,苔原是這裡的地帶性植被,但在熱泉附近卻分布著草甸...
