基本介紹
- 中文名:對角矩陣
- 外文名:diagonal matrix
- 相關:對角方陣
- 定義:是一個主對角線之外的元素皆為 0
- 特殊形式:數量矩陣、單位矩陣
- 套用學科:高等數學
定義
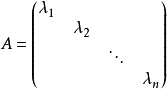
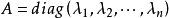
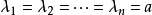
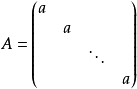
運算規律
和差運算
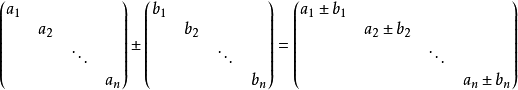
數乘運算

乘積運算
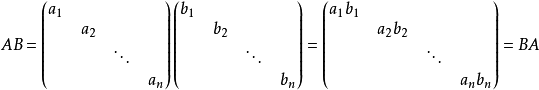
矩陣條件
充要條件
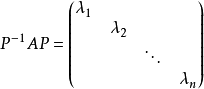
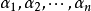
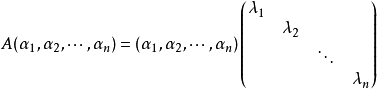
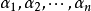
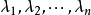
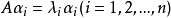
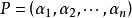
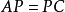
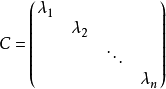
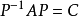

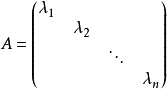
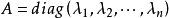
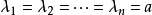
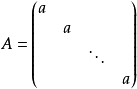
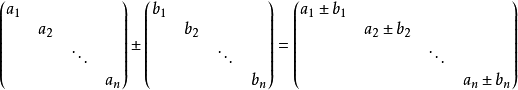

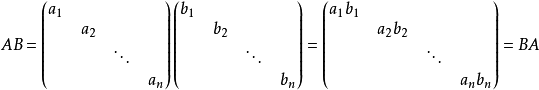
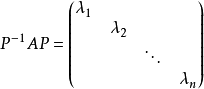
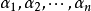
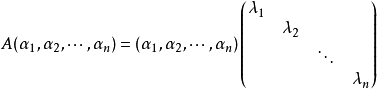
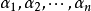
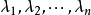
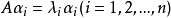
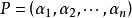
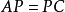
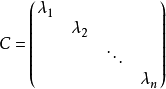
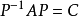
只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。...
對角矩陣(diagonal matrix)是一個主對角線之外的元素皆為0的矩陣,常寫為diag(a1,a2,...,an) 。對角矩陣可以認為是矩陣中最簡單的一種,值得一提的是:對角線...
可對角化矩陣是線性代數和矩陣論中重要的一類矩陣。如果一個方塊矩陣 A 相似於對角矩陣,也就是說,如果存在一個可逆矩陣 P 使得 P −1AP 是對角矩陣,則它就...
線上性代數中,一個n×n矩陣A的主對角線(從左上方至右下方的對角線)上各個元素的總和被稱為矩陣A的跡(或跡數),一般記作tr(A)。...
零矩陣,在數學中,特別是線上性代數中,零矩陣即所有元素皆為0的矩陣。在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及...
在一個n階方陣(或是n階行列式)中,從左上角到右下角這一斜線上的n 個元素的位置,叫做n 階方陣(或行列式)的主對角線。...
一個矩陣稱為下三角矩陣如果對角線上方的元素全部為0。類似地,一個矩陣稱為上三角矩陣如果對角線下方的元素全部為0。...
三角矩陣是方形矩陣的一種,因其非零係數的排列呈三角形狀而得名。三角矩陣分上三角矩陣和下三角矩陣兩種。上三角矩陣的對角線左下方的係數全部為零,下三角矩陣的...
對角線,幾何學名詞,定義為連線多邊形任意兩個不相鄰頂點的線段,或者連線多面體任意兩個不在同一面上的頂點的線段。另外在代數學中,n階行列式,從左上至右下的數...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
列矩陣又稱列向量,是指有一列的矩陣。如果矩陣 A=(aij)m×n只有一行,即m=1,則此時稱之為行矩陣,或行向量。同樣,若 A=(aij)m×n只有一列,即n=1,這時...
