只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。
基本介紹
- 中文名:對角陣
- 外文名:diagonal matrix
- 所屬學科:數學
- 相關概念:矩陣、方陣、線性變換等
定義





分類
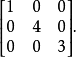

分塊對角陣
線性變換套用
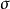
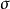

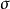

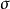




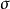

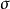


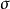

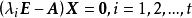
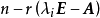

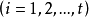


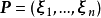












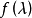









只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。





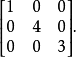

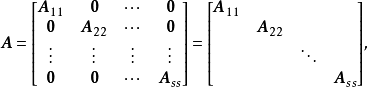
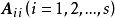

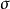

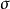




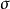

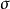


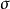

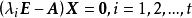
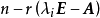

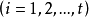


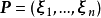












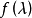








對角矩陣(diagonal matrix)是一個主對角線之外的元素皆為0的矩陣,常寫為diag(a1,a2,...,an) 。對角矩陣可以認為是矩陣中最簡單的一種,值得一提的是:對角線...
只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。...
在一個n階方陣(或是n階行列式)中,從左上角到右下角這一斜線上的n 個元素的位置,叫做n 階方陣(或行列式)的主對角線。...
線上性代數中,一個n×n矩陣A的主對角線(從左上方至右下方的對角線)上各個元素的總和被稱為矩陣A的跡(或跡數),一般記作tr(A)。...
可對角化矩陣是線性代數和矩陣論中重要的一類矩陣。如果一個方塊矩陣 A 相似於對角矩陣,也就是說,如果存在一個可逆矩陣 P 使得 P −1AP 是對角矩陣,則它就...
(1)n階厄米特矩陣A為正定(半正定)矩陣的充要條件是A的所有特徵值大於(大於等於)0。(2)若A是n階厄米特矩陣,其特徵值對角陣為V,則存在一個酉矩陣U,使AU=...
將矩陣分解為簡單矩陣的組合可以在理論和實際套用上簡化矩陣的運算。對一些套用廣泛而形式特殊的矩陣,例如稀疏矩陣和準對角矩陣,有特定的快速運算算法。關於矩陣相關...
包含M矩陣類在內的重要矩陣類,線上性互余及其他許多領域都有廣泛的套用.設A=...1.對每一0≠x∈R,有正對角陣Dx使xDxAx>0.2.A的每一實特徵值皆正.3....
二維數組又稱為矩陣,行列數相等的矩陣稱為方陣。對稱矩陣a[i][j] = a[j][i],對角矩陣:n階方陣主對角線外都是零元素。中文名 二維數組 表達式 a為3*4...
diag函式在FreeMat、Matlab中該函式用於構造一個對角矩陣,不在對角線上元素全為0的方陣,或者以向量的形式返回一個矩陣上對角線元素。...
每一個方陣A(n by n)都相似一個約當陣(Jordan Matrix)。約當陣特點是方陣A的特徵值(eigenvalues)都在對角線上,對角線上方還有若干個1。另外約當陣是由一些約...
海森堡陣是數學用語...... 若i<j-1時,有a(i,j)=0,則稱A是下海森堡陣,容易看出,上海森堡陣的下對角線以下的元素全為零,而下海森堡陣的上對角線以上的元素...
