基本介紹
- 中文名:埃爾米特多項式
- 外文名:Hermite polynomial
- 分類:計算機
- 類別:正交多項式
- 創始人:夏爾·埃爾米特
- 套用:數學 物理學
定義

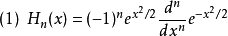

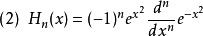

| 序號 | 機率學 | 物理學 |
|---|---|---|
 |  |  |
 |  |  |
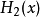 |  |  |
 |  |  |
 |  | 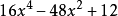 |
 |  |  |
性質
正交性
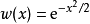




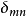
完備性


微分方程



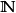


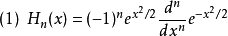

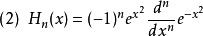

| 序號 | 機率學 | 物理學 |
|---|---|---|
 |  |  |
 |  |  |
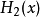 |  |  |
 |  |  |
 |  | 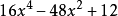 |
 |  |  |
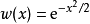




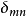






在數學中,埃爾米特多項式是一種經典的正交多項式族,得名於法國數學家夏爾·埃爾米特。機率論里的埃奇沃斯級數的表達式中就要用到埃爾米特多項式。在組合數學中,埃爾...
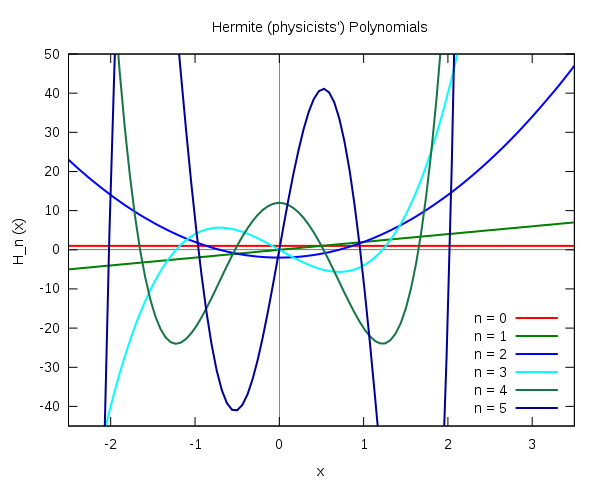
稱Hn(x)為n階埃爾米特多項式。它在[0,+∞)內有n個零點。常用作插值逼近中的結點。...... 為埃爾米特多項式系,而稱Hn(x)為n階埃爾米特多項式。它在[0,+∞...
埃爾米特-費耶爾插值多項式(Hermite-Fejer interpolation polynomials)是埃爾米特插值的一種特殊情況。...
埃爾米特(Charles Hermite,1822—1901)法國數學家。巴黎綜合工科學校畢業。曾任法蘭西學院、巴黎高等師範學校、巴黎大學教授。法蘭西科學院院士。在函式論、高等代數、...
就如許多其他的以人名命名的數學公式一樣,海曼多項式其實也並不是海曼第一個提出的。 拉普拉斯在1810年一篇論文中就給出了埃爾米特多項式的係數,切比雪夫則在 1859...
埃爾米特定理是多項式最大公因式定理的推廣。設f1(x),f2(x),...,fs(x)(s≥2)是數域P上的s個非零多項式,則存在一個𝝀矩陣A(𝝀),它的第一行元素是...
埃爾米特形是多項式矩陣的一種規範形。埃爾米特可分類為行埃爾米特形和列埃爾米特形。任一個多項式矩陣都可通過一系列初等變換或等價單模變換化為埃爾米特形。 ...
正交多項式是由多項式構成的正交函式系的通稱。正交多項式最簡單的例子是勒讓德多項式,此外還有雅可比多項式、切比雪夫多項式、拉蓋爾多項式、埃爾米特多項式等,它們在...
高斯-埃爾米特求積公式(Guass-Hermite)一種高斯型求積公式.指求積區間為(-∞,+∞),權函式的正交多項式為埃爾米特多項式 對應的高斯型求積公式 稱為高斯—埃爾米特...
埃爾米特度量(Hermite metric)是殆複流形上的一種度量。設M是殆複流形,具有殆復結構J。若M上黎曼度量g滿足g(JX,JY)=g(X,Y),這裡X,Y是M上任意向量場,...
不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應的導數值也相等,甚至要求高階導數也相等,滿足這種要求的插值多項式就是埃爾米特插值多項式。...
埃爾米特插值公式(Hermite interpolation formina )區域上解析函式的拉格朗日插值多項式的積分表示式。不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應...
除了一些平凡的例子如 {x} 以外,最值得注意的阿佩爾序列是埃爾米特多項式、伯努利多項式以及歐拉多項式。所有的阿佩爾序列都是謝弗序列,但要注意的是絕大多數謝弗序列...
3.2.4 用計算機軟體求算埃爾米特多項式3.3 勒讓德函式3.3.1 勒讓德方程及勒讓德函式3.3.2 締合勒讓德函式3.3.3 用matlab軟體求算勒讓德函式...
其中H3(x) =x− 3x;H4(x) =x− 6x+ 3 (即埃爾米特多項式)注意到以上的 series 並不保證函式值恆正,所以事實上並不一定是一個密度函式。在許多情況下...
為埃爾米特多項式:注意到不應將之與哈密頓算符搞混,儘管哈密頓算符也標作H。相應的能階為值得注意的是能譜,理由有三。首先,能量被“量子化”(quantized),而只...
在數學領域,高斯函式在埃爾米特多項式的定義中起著重要作用。 高斯函式與量子場論中的真空態相關。 在光學以及微波系統中有高斯波束的套用。 高斯函式在圖像處理中用...
