均值不等式,又名平均值不等式、平均不等式,是數學中的一個重要公式。公式內容為Hn≤Gn≤An≤Qn,即調和平均數不超過幾何平均數,幾何平均數不超過算術平均數,算術平均數不超過平方平均數。
基本介紹
- 中文名:均值不等式
- 外文名:Inequality of arithmetic and geometric means
- 表達式:Hn≤Gn≤An≤Qn
- 套用學科:數學
- 適用領域範圍:不等式
定義
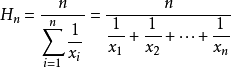
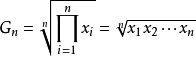
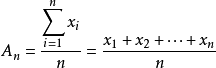
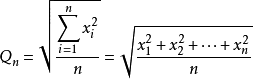
證明
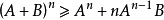
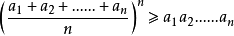
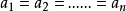
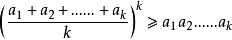
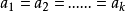
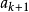
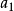
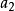
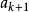

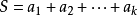

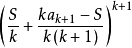
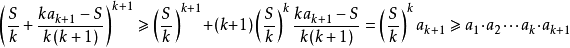



推廣
一般形式
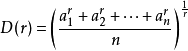
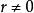
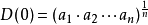
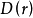
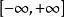
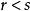
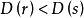
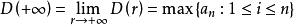
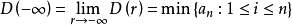

特例
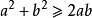

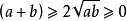
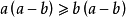
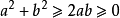
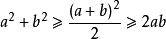

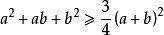
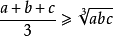
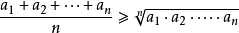
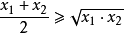
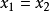
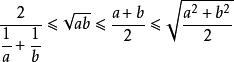
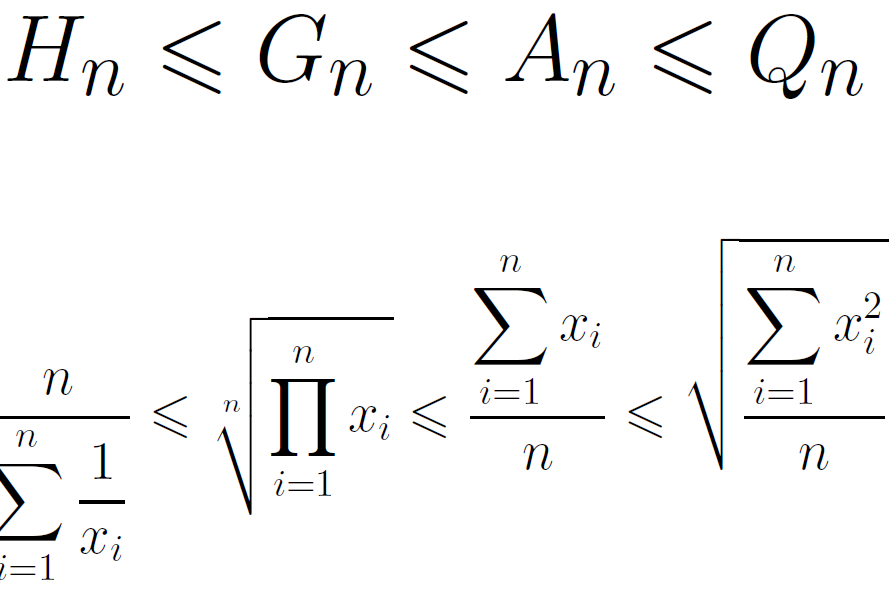
均值不等式,又名平均值不等式、平均不等式,是數學中的一個重要公式。公式內容為Hn≤Gn≤An≤Qn,即調和平均數不超過幾何平均數,幾何平均數不超過算術平均數,算術平均數不超過平方平均數。
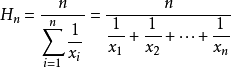
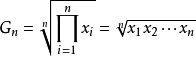
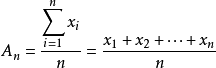
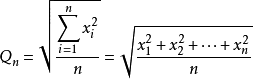
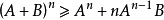
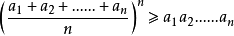
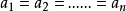
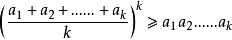
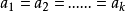
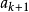
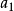
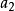
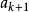

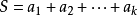

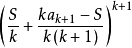
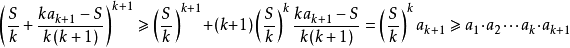



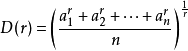
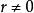
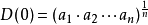
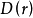
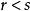
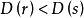
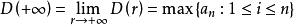
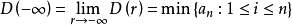

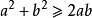

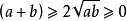
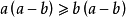
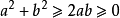
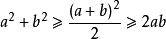

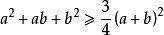
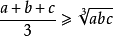
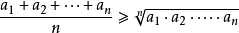
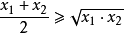
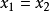
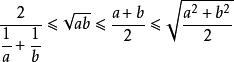
均值不等式,又名平均值不等式、平均不等式,是數學中的一個重要公式。公式內容為Hn≤Gn≤An≤Qn,即調和平均數不超過幾何平均數,幾何平均數不超過算術平均數,算術...
平均數不等式,或稱平均值不等式、均值不等式,是數學上的一組不等式,也是基本不等式的推廣。...
基本不等式是主要套用於求某些函式的最值及證明的不等式。其表述為:兩個正實數的算術平均數大於或等於它們的幾何平均數。...
重要不等式,是指在初等與高等數學中常用於計算與證明問題的不等式。包括,排序不等式、均值不等式、完全的均值不等式、冪平均不等式、權方和不等式、柯西不等式、...
算術-幾何平均值不等式,簡稱算幾不等式,是一個常見而基本的不等式,表現了算術平均數和幾何平均數之間恆定的不等關係。...
均值定理,又稱基本不等式。主要內容為在正實數範圍內,若干數的幾何平均數不超過他們的算術平均數,且當這些數全部相等時,算術平均數與幾何平均數相等。均值定理是...
全稱為Erdos-Mordell(鄂爾多斯—門德爾)不等式,簡稱E-M不等式。...... 由均值不等式(AM-GM不等式)得p,q,r的係數 ≥ 2。故待證不等式得證。...
不等式的證明,基本方法有 比較法:(1)作差比較法 (2)作商比較法 綜合法:用到了均值不等式的知識,一定要注意的是一正二定三相等的方法的使用。 分析法:當...
《輕鬆搞定高中數學不等式》是外語教學與研究出版社出版的圖書,作者是王金戰。...... 第1課 時不等關係與不等式第2課 時比較大小第3課 時均值不等式...
在數學領域, 馬勒不等式陳述說由兩個無窮正項序列的對應項的和構成序列的幾何均值大於或等於這兩個無窮序列幾何均值的和。不等式以庫爾特·馬勒的名字命名。...
《數列與不等式》是2014-1-1 出版的圖書,作者是甘志國 。...... §27.用均值不等式求最值時要注意“一正二定三等”的條件∥223§28.《不等式》練習題∥226...
數學競賽中產生了許多不等式,不等式的證明很多無法搬用固定的方法,但是重要不等式是證明不等式的重要手段,是初學者的入門鑰匙,希望中學生能夠從中獲得收益,也希望...
加強不等式是一種數學方法 為了證明一個不等式,通常現有的方法無法將公式套上去時,可以引入加強不等式,通常要有一定的做題經驗才能準確判斷該加強到什麼地步. 加強...
在高中數學學習中,除了日常的絕對值不等式和基本不等式外,在解決已知x與y關係,求關於x,y分式問題時,可以運用hxq不等式。hxq不等式的基本形式為a/b+c/d≥(√...
《數學奧林匹克不等式證明方法和技巧》是2011年哈爾濱工業大學出版社出版的圖書,作者是蔡玉書。本書主要介紹了比較法證明不等式、聯用均值不等式和柯西不等式證明不...
本書是清華大學附屬中學針對大學自主招生開設的校本課程“不等式選講”的教材,該...第1講不等式基礎知識整合3第2講均值不等式套用技巧8第3講柯西不等式及其套用12...
5.聯用均值不等式和柯西不等式證明不等式 6.柯西不等式的推廣、Holder不等式及其套用 7.不等式■的推廣及其套用 8.Jensen不等式及其套用 9.排序不等式與Chebyshe...
