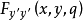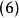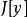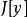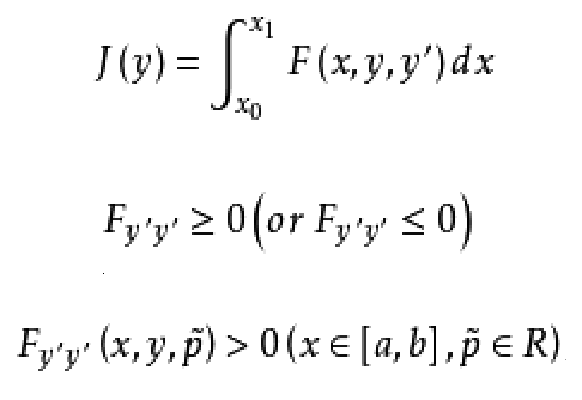定義
稱其為
勒讓德條件。此外,若沿著場的平穩曲線滿足條件
,則稱為
嚴格勒讓德條件。若
相關介紹
對於一個給定的最簡泛函,要檢驗魏爾斯特拉斯條件是否成立,一般情況下比較困難。所以希望能用一個比較簡單的條件來代替魏爾斯特拉斯條件。
設最簡泛函
式中,被積函式
具有連續二階偏導數。將被積函式
關於變元
在
處展成泰勒公式
可見
與
具有相同的符號,故魏爾斯特拉斯條件可用下面的條件來代替
式(6)是勒讓德於1786年通過研究二次變分提出來的,稱為泛函式(1)的勒讓德條件。如果式(6)是嚴格的不等式,則稱為勒讓德強條件。勒讓德條件也是泛函取得極值的必要條件。泛函的一條極值曲線包含在極值曲線場中的充分條件是必須滿足勒讓德強條件。
相關定理
設泛函
,其邊界條件為
,其中
具有連續二階偏導數,並設
為該泛函的極值函式,若滿足下列條件:
例題解析
解: 。當
時,勒讓德條件成立。當
時,勒讓德強條件成立。
例2 設泛函
。試判斷該泛函的極值曲線是否能包含在一個相應的極值曲線場中。
解:因泛函只是
的函式,故其歐拉方程為
,由邊界條件得
,於是極值曲線為
,相應的極值曲線場為
。此時,勒讓德強條件為
若使勒讓德條件成立,應有
,即只有當
時,極值曲線才能包含在
的極值曲線場中。