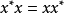基本介紹
- 中文名:八元數
- 外文名:Octonion
- 德文:Oktaven
- 屬於:四元數的推廣
歷史,定義,凱萊-迪克松構造,法諾平面記憶,共軛、範數和逆元素,性質,概述,自同構,參見,
歷史
定義
八元數可以視為實數的八元組。每一個八元數都是單位八元數{1,i,j,k,l,il,jl,kl}的線性組合。也就是說,每一個八元數x都可以寫成 其中係數xa是實數。
其中係數xa是實數。

| 1 | i | j | k | l | il | jl | kl |
|---|---|---|---|---|---|---|---|
| i | −1 | k | −j | il | −l | −kl | jl |
| j | −k | −1 | i | jl | kl | −l | −il |
| k | j | −i | −1 | kl | −jl | il | −l |
| l | −il | −jl | −kl | −1 | i | j | k |
| il | l | −kl | jl | −i | −1 | −k | j |
| jl | kl | l | −il | −j | k | −1 | −i |
| kl | −jl | il | l | −k | −j | i | −1 |
凱萊-迪克松構造
一個更加系統的定義八元數的方法,是通過凱萊-迪克松構造。就像四元數可以用一對複數來定義一樣,八元數可以用一對四元數來定義。兩對四元數(a,b)和(c,d)的乘積定義為:


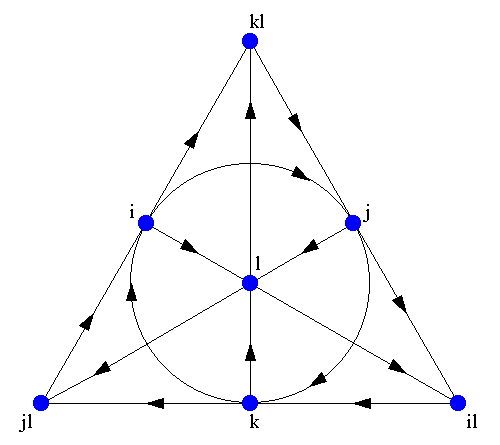
法諾平面記憶
一個用來記憶八元數的乘積的方便辦法,由右面的圖給出。這個圖中有七個點和七條直線(經過i、j和k的圓也是一條直線),稱為法諾平面。這些直線是有向的。七個點對應於Im(O)的七個標準基元素。每一對不同的點位於唯一的一條直線上,而每一條直線正好通過三個點。
共軛、範數和逆元素
八元數


共軛是O的一個對合,滿足 (注意次序的變化)。
(注意次序的變化)。

x的實數部分定義為½(x+x) =x0,虛數部分定義為½(x-x)。所有純虛的八元數生成了O的一個七維子空間,記為Im(O)。
八元數x的範數定義為:

O上範數的存在,意味著O的所有非零元素都存在逆元素。x≠ 0的逆元素為:


性質
概述
八元數的乘法既不是交換的:


然而,八元數確實滿足結合性的一個較弱形式──交錯性。這就是說,由任何兩個元素所生成的子代數是結合的。實際上,我們可以證明,由O的任何兩個元素所生成的子代數都與R、C或H同構,它們都是結合的。由於八元數不滿足結合性,因此它們沒有矩陣的表示法,與四元數不一樣。
八元數確實保留了R、C和H共同擁有的一個重要的性質:O上的範數滿足