互質因子算法

互質因子算法（Prime-factor FFT algorithm, PFA），又稱為Good-Thomas算法，是一種快速傅立葉變換（FFT），把N = N1N2大小的離散傅立葉變換重新表示為N1*N2大小的二維離散傅立葉變換，其中N1與N2需互質。變成N1和N2大小的傅立葉變換後，可以繼續遞迴使用PFA，或用其他快速傅立葉變換算法來計算。

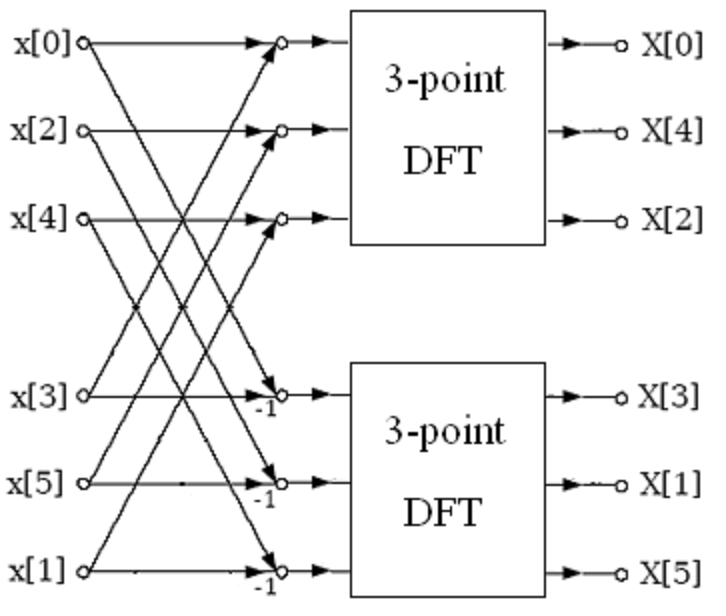
基本介紹

• 中文名：互質因子算法
• 外文名：Prime-factor FFT algorithm
• 縮寫：PFA
• 又稱：Good-Thomas算法
• 本質：一種快速傅立葉變換

簡介

較流行的Cooley-Tukey算法經由mixed-radix一般化後，也是把N = N₁N₂大小的離散傅立葉變換分割為N₁和N₂大小的轉換，但和互質因子算法 (PFA)作法並不相同，不應混淆。Cooley-Tukey算法的N₁與N₂不需互質，可以是任何整數。然而有個缺點是比PFA多出一些乘法，和單位根twiddle factors相乘。相對的，PFA的缺點則是N₁與N₂需互質 (例如N 是2次方就不適用)，而且要藉由中國剩餘定理來進行較複雜的re-indexing。互質因子算法 (PFA)可以和mixed-radix Cooley-Tukey算法相結合，前者將N 分解為互質的因數，後者則用在重複質因數上。

PFA也與nested Winograd FFT算法密切相關，後者使用更為精巧的二維折積技巧分解成N₁ * N₂的轉換。因而一些較古老的論文把Winograd算法稱為PFA FFT。

儘管PFA和Cooley-Tukey算法並不相同，但有趣的是Cooley和Tukey在他們1965年發表的有名的論文中，沒有發覺到高斯和其他人更早的研究，只引用Good在1958年發表的PFA作為前人的FFT結果。剛開始的時候人們對這兩種作法是否不同有點困惑。

算法

離散傅立葉變換（DFT）的定義如下:

PFA將輸入和輸出re-indexing，代入DFT公式後轉換成二維DFT。

Re-indexing

設N = N₁N₂，N₁與N₂兩者互質，然後把輸入n 和輸出k 一一對應到

因N₁與N₂ 互質，故根據最大公因數表現定理，對每個n 都存在滿足上式的整數n₁與n₂，且在同餘N 之下n₁可以調整至0～N₁ –1之間，n₂可以調整至0～N₂ –1之間。並根據同餘理論易知滿足上式且在以上範圍內的整數n₁與n₂是只有一個的。這稱為Ruritanian 映射 (或Good's 映射)，

舉例來說:

如果對於任一都可以對應到

因N₁與N₂互質，故根據中國剩餘定理，對於每組 (k₁,k₂) (其中k₁在0～N₁– 1之間,k₂在0～N₂– 1之間)，都有存在且只有一個的k在0～N- 1之間且滿足上兩式。這稱為CRT映射。CRT映射的另一種表示法如下

其中N₁表示N₁在模N₂之下的反元素，N₂反之。

( 也可以改成對輸入n用CRT映射以及對輸出k用Ruritanian映射)

對於有效re-indexing (理想上是達到原地)的方法有許多研究，以減少耗費時間的模運算。

DFT re-expression

表示方法一:

將以上的re-indexing代入DFT公式里指數部分的nk之中，

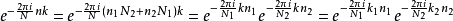
( 因為e= 1，所以兩個指數的k部分可以分別模N₁與N₂)。剩下的部分變成

則內部和外部的總和分別轉換成大小為N₂與N₁的DFT。

表示方法二:

如果令

令相當於取的餘數，

對於每一個都要做一個點的，而因為有個，所以需要個點

對於每一組都要做一個點的而因為為常數，有個，所以需要 個點，

因此如果要計算複雜度，可以乘法器的數量當作考量,

假設點的需要個乘法器,

假設點的需要個乘法器,

則總共需要個乘法器。

與Cooley-Tukey算法的比較

如首段所述，Cooley-Tukey算法和互質因子算法 (PFA)曾被誤認為很類似。兩者皆有各自優點可適用於不同狀況，因此分辨它們的不同是很重要的。在1965年著名的論文中發表的Cooley-Tukey算法，是在DFT的定義

中代入n=n₁+n₂N₁,k=k₁N₂+k₂，則

比PFA多了一些要乘的因子 (稱為twiddle factors)，但index較為簡單，且適用於任何N₁、N₂。在J. Cooley稍後發表的關於FFT歷史探討的論文中使用N= 24點FFT為例，顯示兩種作法在index結構上的不同。