基本介紹
概念
定理概述
例題
其他題目
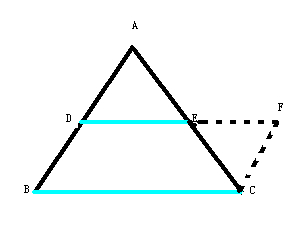
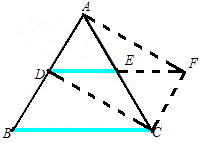
求證:AD與EF互相平分.
證明:連線DE、DF,
∵點D、E分別是BC、AB的中點,∴DE∥AC,
同理得 DF∥AB,
∴四邊形AEDF是平行四邊形,
∴AD與EF互相平分.
逆定理
性質
證明
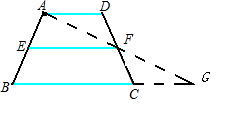 梯形中位線
梯形中位線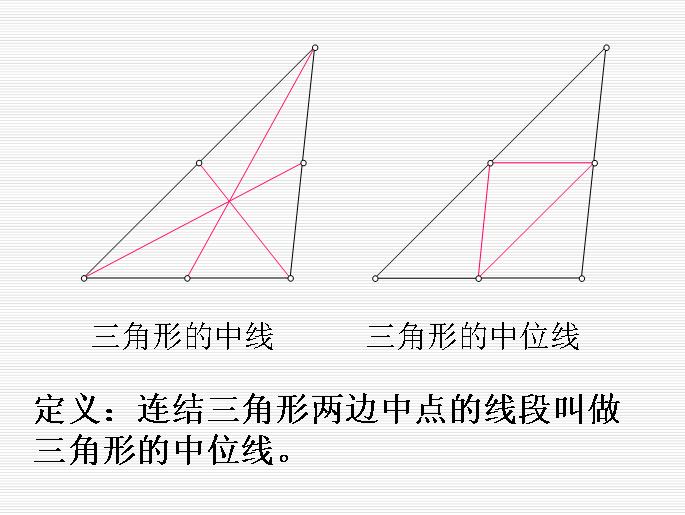


 梯形中位線
梯形中位線連線三角形兩邊中點的線段叫做三角形的中位線,三角形的中位線平行於第三邊並且等於第三邊邊長的一半。連線梯形兩腰中點的線段叫做梯形的中位線,梯形的中位線平行...
連線三角形兩邊中點的線段叫做三角形的中位線。三角形的中位線平行於三角形的第三邊,並且等於第三邊的1/2。三角形中位線定義:連線三角形兩邊中點的線段叫做三角...
中位線是在三角形或梯形中一條特殊的線段,與其所在的三角形或梯形有著特殊的關係。連線三角形的兩邊中點的線段叫做三角形的中位線。三角形有三條中位線,首尾相...
三角形的中位線平行於第三邊(不與中位線接觸),並且等於第三邊的一半。...... 三角形的中位線平行於第三邊(不與中位線接觸),並且等於第三邊的一半。...
中位面,由三角形中的中位線(三角形中位線定義:連線三角形兩邊中點的線段叫做三角形的中位線。)類比多面體而來。 例如,四面體中的中位面為過棱中點的面,四面體的...
∴DE∥AC(三角形中位線定理)∴AC⊥AB,即∠BAC=90°直角三角形斜邊中線定理證法4 向量證明設向量AD=d,向量AB=c,向量AC=b,向量BC=a...
另一個公式:“中位線×高”,其中“中位線”是(上底+下底)除以2。 具有特徵 在直角梯形ABCD中,AD//BC,∠B=90°,則∠A=90°,∠C+∠D=180°。 重要...
4、中位線長是上下底邊長度和的一半,如圖2,中位線為EF,且 。5、兩條對角線相等,如圖2,即 6、等腰梯形的面積公式:S=(上底+下底)×高÷2。...
中位線定理[1] 參考資料 1. 數學定理列表 .維基百科[引用日期2012-12-08] 詞條標籤: 語言, 文化, 數學, 學科 圖集 數學定理列表圖冊 V百科往期回顧 詞條...
②梯形的面積公式: 中位線×高,用字母表示:L·h。③對角線互相垂直的梯形面積為:對角線×對角線÷2。④只知四邊長度時的面積公式:...
