基本介紹
- 中文名:三次曲線
- 外文名:Cubic Curves
- 學科:數學
- 性質:和一般曲線都相交三個點
- 發現者:牛頓
- 定義:F(x,y,z)=0, deg F=3.
曲線介紹
定義
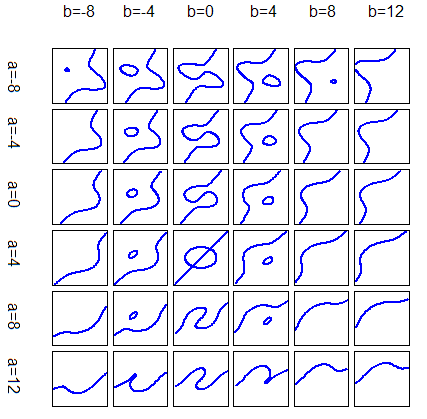 三次曲線
三次曲線 三次曲線
三次曲線數學函式曲線的一種,一條平面代數曲線,顯然, 它和一般的直線都相交三個點。在牛頓之前,也沒有人能夠像把非退化二次曲線分成橢圓、雙曲線與拋物線那樣對三次曲線...
最高次數項為3的函式,形如y=ax³+bx²+cx+d(a≠0,b,c,d為常數)的函式叫做三次函式(cubic function)。 三次函式的圖象是一條曲線——回歸式拋物線(...
本書是一部講述代數曲線的入門書籍,可以作為一二年級數學專業的教程,具備基本的微積分知識可以完全讀懂這本書。通過分類實數上的不可約三次曲線和證明它們的點能夠...
貝塞爾曲線(Bézier curve),又稱貝茲曲線或貝濟埃曲線,是套用於二維圖形應用程式的數學曲線。一般的矢量圖形軟體通過它來精確畫出曲線,貝茲曲線由線段與節點組成,節點...
三次樣條插值(Cubic Spline Interpolation)簡稱Spline插值,是通過一系列形值點的一條光滑曲線,數學上通過求解三彎矩方程組得出曲線函式組的過程。實際計算時還需要...
三次插值法(cubic interpolation method)是一種多項式插值法,逐次以三次曲線φ(t)=a0+a1t+a2t2+a3t3的極小點逼近尋求函式f(t)的極小點的一種方法.具體做法...
所謂樣條曲線(Spline Curves)是指給定一組控制點而得到一條曲線,曲線的大致形狀由這些點予以控制,一般可分為插值樣條和逼近樣條兩種,插值樣條通常用於數位化繪圖...
三次方程的英文名是Cubic equation,指的是一種數學的方程式。三次方程是未知項總次數最高為3的整式方程。三次方程的解法思想是通過配方和換元,使三次方程降次為...
為了能夠套用微積分的知識,我們不能考慮一切曲線,甚至不能考慮連續曲線,因為連續不一定可微。這就要我們考慮可微曲線。但是可微曲線也是不太好的,因為可能存在某些...
標準型的一元三次方程aX^3+bX^2+cX+d=0(a,b,c,d∈R,且a≠0),其解法有:1、義大利學者卡爾丹於1545年發表的卡爾丹公式法;2、中國學者范盛金於1989年發表...
三次樣條插值法cubic spline inter}x}lalic}i}樣條函式中最重要的一種函式。若函式S(二)在區間【。。川的每一分段}x』一,,二,](i=2,3, } ,n)上是...
三次電流分布是指除電化學極化外,深度極化也需考慮時的電流分布稱為三次電流分布,顯然這發生在電流密度達到一定值,電極表面附近的反應物濃度顯著降低,傳質過程已不...
程式設計中的三次法則是代碼重構的一條經驗法則,涉及到當代碼片段出現重複時,如何決定是否用一個新的子程式替代之的標準。...
一般來說,四次函式的圖像並不都像二次函式那樣的拋物線,也不多是三次函式的回歸性拋物線,而是一種全新的非常規曲線,當然,具體的圖像要根據函式解析式得出,待定...
1673年,萊布尼茲首次使用“function”(函式)表示“冪”,後來他用該詞表示曲線上點的橫坐標、縱坐標、切線長等曲線上點的有關幾何量。與此同時,牛頓在微積分的討論...
所謂三階導數,即原函式導數的導數的導數,將原函式進行三次求導,不代表該點的曲率,談幾何意義頂多只能算代表原函式一階導數的凹凸性。...
撓率,它的絕對值度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在一平面上,則稱為撓曲線。在三維曲線...
