限制性三體問題，【作者】趙德滋。三體問題的特殊情況。當所討論的三個天體中﹐有一個天體的質量與其他兩個天體的質量相比﹐小到可以忽略時﹐這樣的三體問題稱為限制性三體問題。一般地把這個小質量的天體稱為無限小質量體﹐或簡稱小天體﹔把兩個大質量的天體稱為有限質量體。
基本介紹
- 書名：限制性三體問題
- 又名：restricted three-body problem
- 作者：趙德滋
- 參考書目：易照華等編著﹕《天體力學引論》
內容簡介,
內容簡介
把小天體的質量看成無限小﹐就可不考慮它對兩個有限質量體的吸引﹐也就是說﹐它不影響兩個有限質量體的運動。於是﹐對兩個有限質量體的運動狀態的討論﹐仍為二體問題﹐其軌道就是以它們的質量中心為焦點的圓錐曲線。根據圓錐曲線為圓﹑橢圓﹑拋物線和雙曲線等四種不同情況﹐相應地限制性三體問題分四種類型﹕圓型限制性三體問題﹑橢圓型限制性三體問題﹑拋物線型限制性三體問題和雙曲線型限制性三體問題。
在小行星運動理論中﹐常按橢圓型限制性三體問題進行討論﹐脫羅央群小行星的運動就是太陽-木星-小行星所組成的橢圓型限制性三體問題的等邊三角形解的一個實例。布勞威爾還按橢圓型限制性三體問題來討論小行星環的空隙。拋物線型限制性三體問題和雙曲線型限制性三體問題在天體力學中則用得很少。人造天體出現後﹐限制性三體問題有了新的用途﹐常用於研究月球火箭和行星際飛行器運動的簡化力學模型﹐見月球火箭運動理論和行星際飛行器運動理論。
以下為“平面圓型限制性三體問題的計算機模擬解”。
採用計算機模擬，建立一個虛擬三體模型。兩個大質量的天體質量分別為M1和M2，第三個天體M0質量為零，這三個天體組成一個封閉系統，僅僅只受萬有引力相互作用，分別設定三個天體的質量、位置和速度，試驗測試其穩定的繞行條件。因為在一個只有萬用引力作用的系統里，質量是重要參數，下文分別以三個天體質量數值M1、M2、M0分別指代三個天體的名稱。M2以一個圓型軌道自西向東圍繞M1運行，M1和M2相距R12。在R12處有一個點，在這個點上受M1和M2的引力相等，這個點稱作引力平衡點，其中M1距M1與M2的引力平衡點R1，M2距M1與M2的引力平衡點R2。M0以圓型軌道繞M2運行，其軌道面與M2繞M1的軌道面相同。M0與M2的距離為R0，當R0小於R12，此時的穩定關係稱為內穩定。當M0同時繞M1和M2共軌道面運行，且R0大於R12時，此時的穩定關係稱為外穩定。如M0繞行方向與M2繞M1相同，都是自西向東，則稱為順向，反之M0的繞向方向從東向西，則稱為逆行。因此三體共軌道面的穩定關係一共有四種：順行內穩定；逆行內穩定；順行外穩定；逆行外穩定。為便於理解，可以把M1想像為地球，M2想像為月球，M0想像為人造衛星。
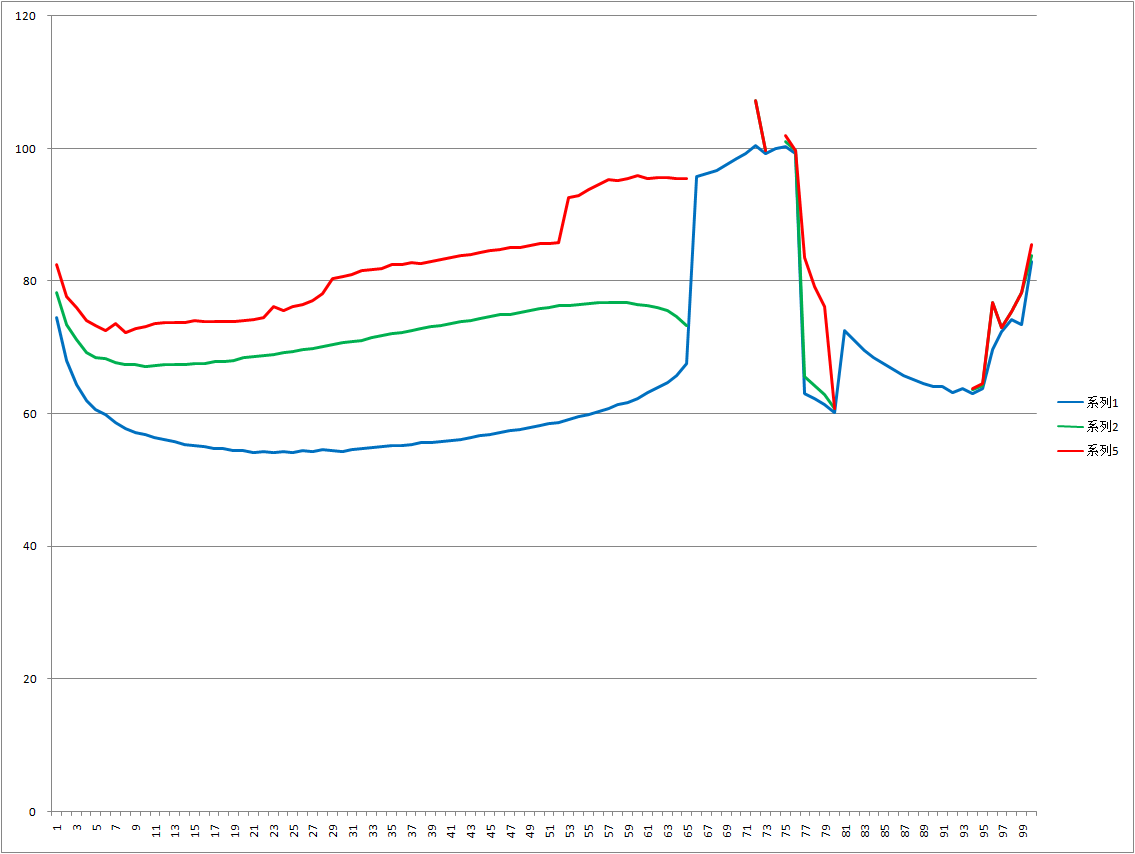
- 初始狀態：M1、M2和M0排列成一條直線，M2以圓型軌道自西向東繞M1運行，M0自西向東繞M2運行，M0=0，M2/（M1+M2）分別設定為1%至99%，R0分別設定為10%R2至120%R2，經過試驗，求得共軌道面順行內穩定曲線如下：
圖中，縱軸為R2，歸算到100%。橫軸為M2占（M1+M2）的百分比。從零至藍線區域（在M2的引力範圍R2的50%區間以內），都是穩定的，藍線與綠線之間有一巨大的不穩定間隙，綠線與紅線區域是穩定的，紅線再往上則不再穩定。M2質量占比在66%至76%這一區間，穩定區域不穩定間隙消失，穩定區間擴大到接近100%R2，局部超過100%R2。穩定曲線不受總質量的影響，只受質量分配的影響。曲線不是光滑的，即在穩定區與不穩定的邊界處，有許多間斷，即有多個不穩定間隙。
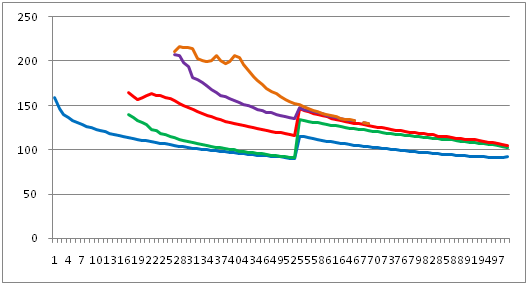
- M2以圓型軌道自西向東繞M1運行，M0自東向西繞M2運行，M0=0，M2/（M1+M2）分別設定為1%至99%，R0分別設定為10%R2至200%R2，經過試驗，求得共軌道面逆行內穩定曲線如下：
圖中，縱軸為R2，歸算到100%。橫軸為M2占（M1+M2）的百分比。從零至藍線區域（在M2的引力範圍R2的90%區間以內），都是穩定的，藍線與綠線之間有一巨大的不穩定間隙，綠線與紅線之間區域是穩定的，紅線再往上與紫線之間又有一不穩定間隙，紫線與橙線之間仍然是穩定區。M2質量占比在53%處，曲線有一大轉折跳躍。穩定曲線不受總質量的影響，只受質量分配的影響。曲線不是光油的，即在穩定區與不穩定的邊界處，有許多間斷，即有多個不穩定間隙。
