基本介紹
- 中文名:遞推列
- 外文名:recursive sequence
- 別稱:遞歸列
- 所屬學科:數學(線性代數)
- 簡介:由前面的項能推出後面的項的數列
基本介紹

相關介紹

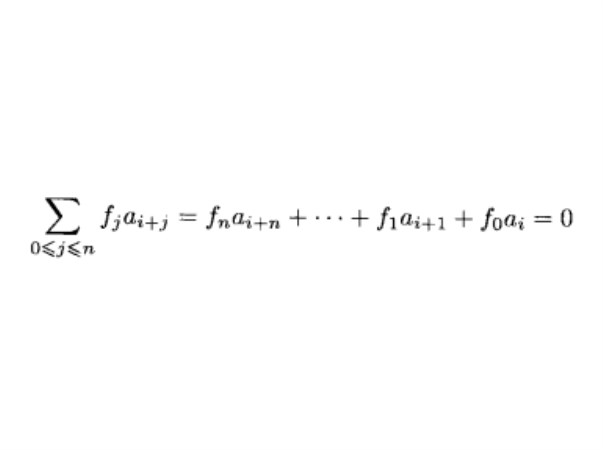


遞推列(recursive sequence)亦稱遞歸列,指由前面的項能推出後面的項的數列,線性遞推列是特殊的遞推列。例如等差數列與等比數列就是遞推列,也是線性遞推列。...
如果數列{an}的第n項與它前一項或幾項的關係可以用一個式子來表示,那么這個公式叫做這個數列的遞推公式。...
遞推數列是可以遞推找出規律的數列,找出這個規律的通項式就是解遞推數列。求遞推數列通項公式的常用方法有:公式法、累加法、累乘法、待定係數法等共十種方法。....
《遞推數列》是2014年中國科學技術大學出版社出版的圖書。...... 《遞推數列》是2014年中國科學技術大學出版社出版的圖書。書名 遞推數列 又名 叢書名稱:數林外傳...
《遞推與遞推方法》是2008年7月由華中科技大學出版社出版的圖書,作者是李世傑。該書主要講述了遞推與遞推方法。...
常係數線性遞推數列,由初始值和下述形式的方程A(n+k)=F(A(n+k-1),...A(n))---1確定...
《新課標下的遞推數列》是2010年6月出版的圖書,作者是黃顯甫。...... 《新課標下的遞推數列》是根據高中數學新課程標準編寫的,介紹了特殊數列的求和、遞推數列的...
在數學上,斐波那契數列以如下被以遞推的方法定義:F(1)=1,F(2)=1, F(n...(注:奇數項和偶數項是指項數的奇偶,而並不是指數列的數字本身的奇偶,比如從...
我們看到,“每段的長度不小於1”這個條件起了控制全局的作用,正是這個最小數1產生了斐波那契數列,如果把1換成其他數,遞推關係保留了,但這個數列消失了。這裡,...
對於求解線性遞推數列,我們還經常使用生成函式法,而對於常係數線性遞推數列,其生成函式是一個有理分式,其分母即特徵多項式。為n*n的矩陣A的特徵多項式為|A-λE...
同樣我們還可以有t階斐波那契數列,通過遞推數列a(n+t)=a(n+t-1)+a(n+t-2)+...+a(n),其中a(1)=a(2)=1,以及對於3-t<=n<=0,有a(n)=0....
全錯位排列遞推數列法 對於排列數較多的情況,難以採用枚舉法。這時可以用遞歸思想推導錯排數的遞迴關係式。顯然 , 。當 時,不妨設n排在了第k位,其中k≠n,...
同時介紹了一維、二維線性遞推序列以及Rinrdan陣列與矩陣變換和矩陣的冪,試圖對前人在組合序列與矩陣的關係上的研究成果進行較系統的歸類總結。 [1] ...
▪ 遞推公式 ▪ 通項公式 2 程式實現 近半數列簡介 編輯 近半數列定義 近半數列指的是這樣一個數列1/4,3/8,7/16,15/32,31/64 ...這個數列從第...
第6課時 遞推數列的通項公式 第7課時 數列的求和 第8課時 數列與不等式 第9課時 數列與算法 第10課時 數列與其它知識的綜台 第11課時 數列的實際套用 第12...
這類題型的命題背景十分簡單,只需要給出一列數字,少數情況下會涉及圖形,考查...遞重數列基礎遞推數列//72遞推和及其修正//175遞推方及其修正//78遞推積...
二、以遞推數列為模型的套用題 27 三、分期付款問題 30 第三章 特殊數列求和 33 一、分組求和 33 二、拆(裂)項求和 35 三、轉化成等差、等比數列求...
3.4 高階遞推數列的有界性和單調性問題第4章 周期數列4.1 基本概念4.2 判定周期性的方法4.3 和數列的周期性4.4 周期點列4.5 函式疊代和周期點...
第2章遞推數列與高階等差數列2.1數列的通項2.1.1通項公式的定義...6.2點列問題6.2.1知識要點6.2.2範例解析6.3分組數列及其套用...
《數學奧賽輔導叢書(第2輯):有趣的差分方程(第2版)》將高中的數列與遞推知識作為基本起點,從斐波那契數列等趣味問題開始,引入差分方程的理論與方法,研究差分...
第六章 遞推數列第一節 遞推數列綜合介紹第二節 整體趨勢法第三節 遞推聯繫法第四節 題型拓展第七章 圖形數陣第一節 圓圈題...
3. 求遞推數列a(1)=1,a(n+1)=1+1/a(n)的通項公式由數學歸納法可以得到:a(n)=F(n+1)/F(n),將費波納茨數列的通項式代入,化簡就得結果。...
6. 非線性遞推點列極限問題的探討.《數值方法及算例》電子工業版社1992.1.7. 關於貝努里方程的常數變異發及其推廣.《數學學習》1992,NO1~2....
2.2 遞推數列2.3 數列與函式2.4 數列中不等式的證明2.5 數列中的探究性問題第3章 解析幾何3.1 求基本量(a, b, c, e, p)或方程...
第5節遞推數列 第6節數列的補遺、綜合題 第10章不等式 第1節不等關係...第1節離散型隨機變數及其分布列 第2節條件機率,相互獨立事件的有關機率 第...
同樣我們還可以有t階斐波那契數列,通過遞推數列a(n+t)=a(n+t-1)+a(n+t-2)+...+a(n),其中a(1)=a(2)=1,以及對於3-t<=n<=0,有a(n)=0. ...
分式線性遞推數列若干問題的統一處理 // 7分式線性遞推數列通項的一種求法 // 13三次遞歸數列通項可求的兩種情形 // 16二次分式遞歸數列通項可求的情形 /...
附錄3高斯的算術幾何平均數列,附錄4數列的斂散性與疊代過程,附錄5數列極限的證法,附錄6-遞推數列的幾何解法及推廣,附錄7吉米多維奇《數學分析習題集》的幾個習題...
