西爾維斯特-加萊定理

西爾維斯特–加萊定理（Sylvester–Gallai theorem）說明若在平面上有有限數目的點，點的數目多於2，它們不是全部共線，有一條線上剛好有兩點，如果過任意兩點的直線都必過第三點，則所有的點共線。

這個定理在無限點的情況並不成立。

基本介紹

• 中文名：西爾維斯特-加萊定理
• 外文名：Sylvester–Gallai theorem
• 分類：數理科學

證明

以下使用無窮遞降法：

1.在平面上有有限多點，若它們都共線，那我們就找到想要的東西；若非，定義一條“連線”為一條連起來至少有兩點的線。設I為一條連線，因為不是所有點都共線，至少有一點P不屬於I。

2.若I不是有剛好兩點，I便至少有三點，稱為A,B,C。不失一般性，設B在A和C之間，因為，所以兩隻角不可能同時是鈍角。不失一般性設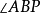不是鈍角，而是銳角或直角。

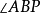
3.設連結C和P的線為m，m是不包括B的連線，而且B和m的距離比P和I的距離小。

4.以B和m取代第二步的P和I。這個動作不可能無窮次重複，因為若能無窮次重複，連線和某一不在連線上的點距離便會得出一個無窮遞降的序列，但只有有限個點和有限條連線，這是不可能的。因此，至少有一條線剛好有兩點。

推廣

這個定理說明了在所有點至少有一條線有剛好兩點。在什麼情況下，只有一條線有剛好兩點呢？沒有的這樣的例子。Dirac猜想在平面上若有n點，則有至少有n/2條線有剛好兩點。

可惜這個猜想是不對的。但截至2006年，已知有兩個反例：

• 一個等邊三角形的三個頂點、各邊的中點和三角形中心，共有7點，但只有三條線有剛好兩點。
• 兩個大小相等的正五邊形，其中一邊重疊。取這兩個五邊形的所有頂點（8點），加上重疊邊的中點（1點），再加上取四組平行線上的無限遠點（4點）。該四組平行線分別是跟重疊邊成0°、90°、+36°和-36°的。在經過這13點的線中，只有6條線有剛好兩點。

雖然Dirac的猜想不對，但有較弱的結果：在n點中，至有有條線剛好有兩點通過。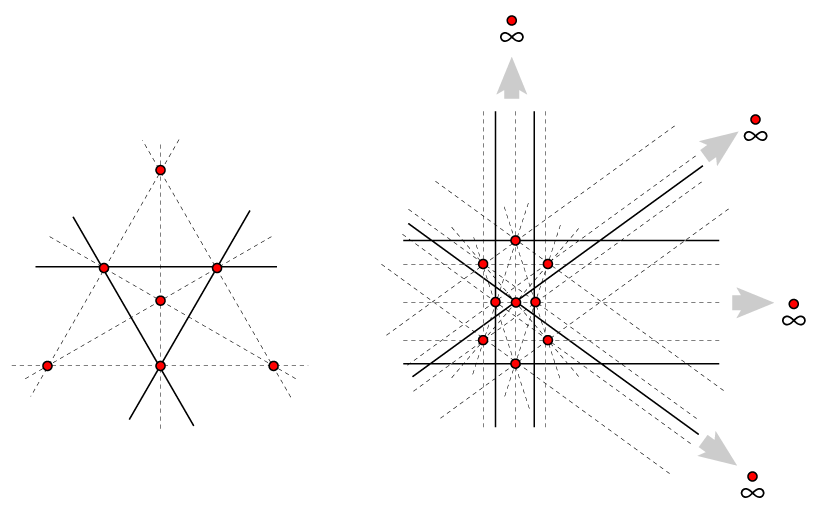

Beck定理則說明了，存在常數C,K，使以下其中一個論述為真：

• 有一條線有n/C點。
• 至少有n/K條線，線上至少有兩點。

歷史

1893年，詹姆斯·約瑟夫·西爾維斯特將此問題提出。保羅·艾狄胥也曾在1943年獨立提出這個定理。1944年蒂博爾·加萊發表了的證明。 不過，1940年E. Melchior已證明了。