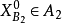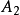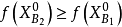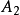規劃介紹
組合最最佳化是通過對數學方法的研究去尋找處理離散事件的最優編排、分組、次序或篩選等問題的最佳化方法。組合最最佳化實際上就是從有限個離散狀態中選取最好的狀態。這種最佳化問題一般可以描述為
我們稱這種最佳化問題為組合最佳化問題。現實中的大量最佳化問題就是從有限個狀態中選取最好的狀態,因此,大量的實際最佳化問題是組合最佳化問題。最最佳化問題一般分為兩大類:一類是具有連續型的變數,另一類是具有離散型的變數,後一類被稱為組合最最佳化,組合最佳化問題有時又稱為離散最佳化(Discrete Optimization)問題。
實際上,上述組合最佳化問題是一個規劃問題。解決這類最佳化問題的方法有各種規劃(線性、非線性、目標、整數、隨機、模糊)、遺傳算法、退火算法、神經網路、搜尋算法、拉格朗日鬆弛算法等。
一個組合最最佳化問題可以用3個參
表示,其中D表示決策變數的定義域,F表示可行解區域,F中的任何一個元素稱為該問題的可行解,
表示目
標函式。組合最最佳化的特點就是可行解集合為有限點集。由直觀可知,只要將定義域D中的有限個點逐一判別是否滿足約束,並比較目標函式的大小,就可以得到該問題的最優解,這就是枚舉法。對於某些最佳化問題可以通過枚舉法得到最優解,這在問題規模較小時是十分有效的,也是非常全面的。但對於複雜的問題,枚舉法顯然是無法接受的。每一個組合最最佳化問題都可以通過枚舉的方法求得最優解,然而枚舉是以時間為代價的,有的枚舉時間還可以接受,有的則不可能接受。
有的最佳化問題是有實時性要求的,如作戰決策、天氣預報等。因此,在這種情況下,對於最佳化問題還要附加時間性要求。
比如典型的旅行商(Traveling Salesman Problem,TSP)問題,若採用枚舉法,則計算時間如表1所列。
城市數 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
計算時間 | 1s | 24s | 10m | 4.3h | 4.9d | 136.5d | 10.8a | 325a |
註:s表示秒;m表示分;h表示小時;d表示天;a表示年 |
對於這種問題至今為止還沒有找到一種求最優解的算法,而這些組合最最佳化問題又有非常強的實際套用背景。因此,人們不得不嘗試採用一些並不一定能保證可以求得最優解的算法來求解組合最最佳化問題,我們稱之為啟發式算法。
組合最最佳化包含了許多常用的但一般很難處理的著名問題,像最短路問題、最小樹問題、匹配問題和旅行售貨員問題,也都屬於組合最最佳化問題。下面介紹一些典型問題並介紹幾種基本方法。
背包問題
有n件東西重量為
,價格為
,要求從中選出若干件裝入背包,即使總重量不超過M,又使總價值最大。
Greedy算法:將比值
由小到大排好隊逐件考慮,不超重就裝入,否則放棄,考慮下一件。
算法的實質就是“挑好的裝,裝進後就不再換出”。不過,一般這種方法不一定能求得最優解。其實背包問題是NP-Complete問題,至今沒有有效解法。
匹配問題
Greedy算法對背包問題不能保證求得最優解,但是能求得一個比較好的初始解。人們通常以它為基礎再作一些調整。例如,嘗試用兩件東西去換1件或3件去換2件等辦法來改進所求的解。交錯鏈方法就是這種樸素思想的發展,它是組合最最佳化方法的核心。
下面通過匹配問題來說明交錯鏈方法。
有n個工人和n項工作,每個人只能適應其中某幾項工作。要求尋找一種分配方式,使得儘可能多的人分配到適應的工作崗位上。
例如,有5個工人:A、B、C、D、E,5項工作1,2,3,4,5,各工人與各工作之間的適應關係如圖1所示。圖中有線段相連表示適應。例如,A適應於1和2,問最多能同時安排幾個人的工作?
從圖上看,是要求利用線段將圖中的端點一一配對,且希望配得對數越多越好。這就是圖論中最大匹配問題。可見,所謂匹配就是無公共頂點的邊所組成的集合。
首先,通過直覺觀察,求出一個較好的初始匹配方案。在圖中用粗線段標出,如圖2所示。這時已連上粗線段的點稱為已蓋點,尚未連粗線的點稱為未蓋點,圖上的一條路,若路上的線段粗細交錯,則稱其為交錯鏈,如圖3所示。稱連線兩個未蓋點的交錯鏈為增廣鏈。對於增廣鏈,細線段比粗線段多一條。對給定的匹配方案
,假若存在一增廣鏈S,那么只要把路S上的細線和粗線交換一下,便可得到多安排一個人的新匹配方案
。通常用下述符號表示上述調整運算:
定理1 一個匹配為最大匹配的充要條件是不存在關於它的增廣鏈。
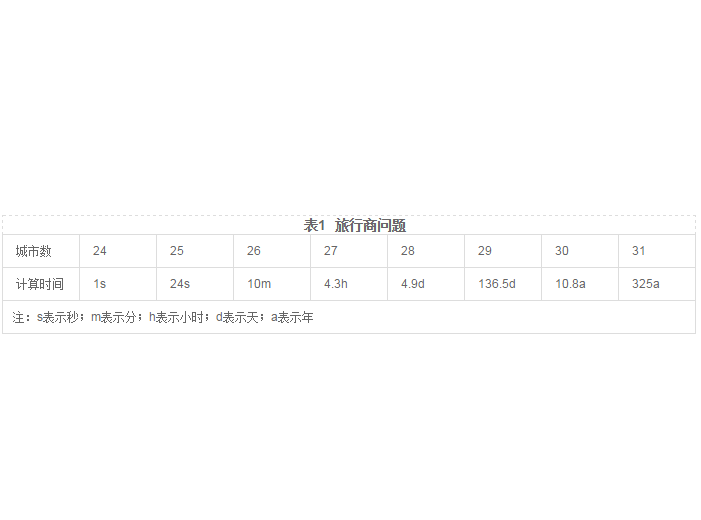
如何尋找增廣鏈?採用“樹生長法”(或稱標號法),以圖2為例,開始任取一未蓋點為樹根,如D,從樹根沿著細線生長,接著從樹梢出發沿著粗線往外生長,這樣交錯地沿著細線和粗線繼續從樹梢往外延伸,直到不能再生長(如圖4)。稱圖4是以D為根的交錯樹。在樹的生長過程中,一旦發現除樹根外,另一未蓋點被長到樹上,過程就可中止。這時樹上連結兩個未蓋點的那條路,便是一條增廣鏈。圖4中D與⑤之間就是一條增廣鏈,沿著它們調整後,可得匹配圖5。
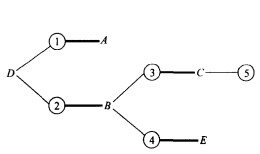 圖4
圖4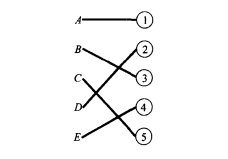 圖5
圖5總結交錯鏈方法的計算步驟如下:
1.任選初始的匹配圖;
2.利用樹生長法尋找增廣鏈。如果找到一條增廣鏈則轉步驟3;如果所有交錯樹上都無增廣鏈,則步驟終止,已找到最大匹配;
3.(調整)替換增廣鏈上的粗線和細線,得到一個新的匹配圖,然後轉步驟1。交錯鏈方法的計算量是
。
排序問題
在許多可能的順序中找一個最優順序,分配加上加工順序的限制,就成排序問題。例如,A與B兩車床加工n件產品,加工時間分別為
和
。A先加工,然後B再加工,問如何安排所用時間最少?
由於加工順序是A先B後,故應儘量減少B的等待時間。因此,不難理解其最優方案應是每次從{
)中取出一個最小值,若它屬於{
},則應排在最先加工,若屬於{
),則應排在最後加工,然後對已確定加工順序的數據從{
)中去掉。在余集上重複上述過程,依次排列,便得最優排序。此問題也可用動態規劃的方法求解。
上述是2×n的同順序排序問題,對於一般的m×n(m>3)的同順序排序問題及不同順序的排序問題,要用“分枝定界法”求解,現將該方法簡介如下:
分枝定界法
欲求
考慮求
其中:要求
,稱式(2)為式(1)的鬆弛問題,它容易求解。若式(2)的最優解
,則
;否則,分A為兩個(或多個)子集:
,解相應的鬆弛問題:
;若
,則
問題已解決(否則,對
重複A的過程)。同樣若
,則
問題已解決,從而
即為所求最小值。若
而
(但
),則
也不必考慮了;否則,對
繼續實行如同A的步驟,如此進行,直到求得最優值為止(
取最小的子集先考慮)。
郵遞員問題
一個郵遞員負責投遞某個街區的郵件,現在需要為他設計一條最短的線路,從郵局出發,經過投遞區內每條街道至少一次,最後返回郵局。一般說來,為了經過每條街道至少一次,有些街道可能需要重複通過,如果限制每條街道不得通過三次或三次以上(可以證明某段街道通過三次或三次以上的投遞路線一定是可以簡化的),那么所有可能的投遞路線的總數就是有限的,也就是說中國郵遞員問題的可行解個數是有限的,因此它是一個組合最最佳化問題,這個問題是我國
管梅谷教授在1960年首先提出的,所以在國際上被稱為“中國郵遞員問題”,中國郵遞員問題已被公認為重要的組合最最佳化問題之一。
售貨員問題
某公司的商品推銷員打算從城市1出發,走遍城市2,3,…,n,去推銷商品,最後回到城市1。問如何安排他的旅行路線,使走的路線的總長度最短(有時我們加上“經過每個城市恰好一次”這樣的限制),這個問題稱為旅行售貨員問題。
旅行售貨員問題的研究已經有四十多年的歷史了,是組合最最佳化問題中另一個重要的研究課題,比較一下旅行售貨員問題和中國郵遞員問題是很有趣的,它們的提法看上去很相似,但實際上有本質的區別。
最小連線問題
給定n個城市。現在需要架設通訊線路,把這n個城市都連線起來,假定架設連線城市i和城市j的通訊線路所需費用為
,問應該在哪些城市之問架設線路,既能使所有城市之間都能連通,又要總的架設費用最小?這個問題等價於最小樹問題。

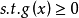




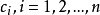




 圖4
圖4 圖5
圖5