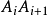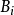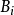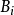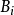基本介紹
不在同一個平面內的若干線段(至少有四條),首尾相接,並且最後一條的尾端和最初一條的首端重合,這樣組成的圖形叫做“空間多邊形”。例如,
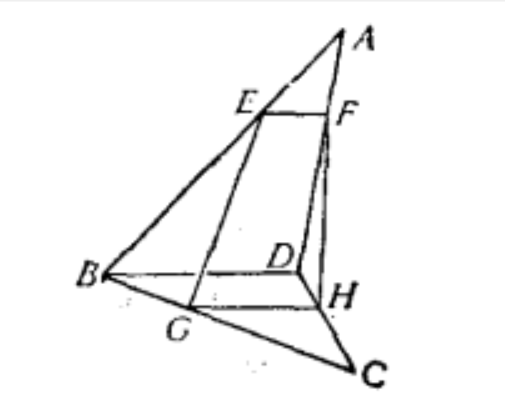
空間四邊形就是最簡單的空間多邊形。
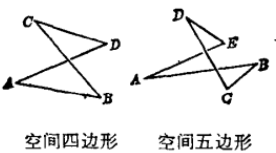 圖1
圖1【例1】 試證內接於空間四邊形的任何平面四邊形的對邊如果相交,那么交點必定在空間四邊形的對角線上。
 圖2
圖2已知:如圖2,空間四邊形ABCD,又平面四邊形PQRS的頂點P、Q、R、S分別線上段AB、AD、CD、CB上,且PQ∩SR=K。
求證:K∈BD。
證明 ∵ P∈AB,Q∈AD,K∈PQ,
∴PQ⊂平面ABD,∴ K∈平面ABD,
同理K∈平面BCD,∴K∈BD。
說明:怎樣證明點在直線上?本題告訴我們,如果要證明點在兩個平面的交線上,那么只需要證明這個點既在第一個平面上又在第二個平面上即可。
相關結論及證明
空間四邊形
1.證明:空間四邊形各邊的中點是平行四邊形的頂點。
提示 設A1,B1,C1和D1是邊AB.BC,CD和DA的中點,則A1B1 // AC和C1D1// AC,所以A1B1//C1D1(特別地,點A1,B1,C1和D1在一個平面上),類似地B1C1// A1D1。
2.證明:問題1中的平行四邊形的中心與連線四邊形對角線中點的線段的中點重合。
提示 設A1,B1,C1和D1是邊AB,BC,CD和DA的中點。再設P和Q是對角線AC和BD的中點,則線段A1Q和PC1平行於線段AD,同時這兩個線段每一個的長等於線段AD長的一半,因此A1PC1Q是平行四邊形,所以線段A1C1的中點與線段PQ的中點重合。
3. 證明:空間四邊形ABCD的對邊兩兩相等,若且唯若它們的對角兩兩相等。
提示 如果AB=CD和BC=AD,那么三角形ABC和CDA全等,所以∠ABC=∠CDA,類似有∠BAD=∠DCB.。
現在假設∠ABC=∠CDA和∠BAD=∠DCB,我們考察四面體abed,它的界面垂直於四面體ABCD的邊,也就是AB⊥bed,BC⊥cda,CD⊥dab和DA⊥abc,根據條件平面bcd和cda之間的角等於平面dab和abc之間的角,即,棱ad上的二面角等於棱ab上的二面角。此外,棱bc上的二面角等於棱ad上的二面角,由兩對二面角的等式推得三面角abcd和cdba的相等(這兩個三面角在棱ac上的二面角是公用的),由三面角的等式推得它們對應的面角相等,特別地,∠bac=∠dca 和∠acb=∠cad,所以 △abc≌△cda,類似地,△dab ≌△bcd。
廣梅涅勞斯定理
4. 一個平面交空間多邊形
(或它們的延長線)於點
;點
在直線
上,證明
並且在多邊形的邊上(而不在它的延長線上)有偶數個點
。
提示 我們考察在垂直於已知平面的直線上的射影。所有的點
此時的射影在一個點B,而點
的射影在點
因為在射影變換下保持在一條直線上的線段的比例,那么
已知平面分空間為兩部分,由頂點
走到
,我們由空間的一個部分變到另一個部分,僅當點
在邊
上。因為,完成多邊形的迴路我們返回到空間的起始的部分,那么位於多邊形邊上的點
的數目是個偶數。
5. 在空間四邊形ABCD的邊AB,BC,CA和AD上分別取點K,L,M和N,證明:這些點在一個平面上,若且唯若
提示 我們考察點N',它是平面KLM與直線DA的交點。根據問題4有
根據同一個問題點N'線上段AD上,因為點K,L和M在四邊形的邊上,而不在它們的延長線上。
點K,L,M和N在一個平面上若且唯若N=N'。所以線上段AD上的兩個點N和N',有N=N'若且唯若DN':AN'=DN:AN。
其他問題
6.已知頂點為
的空間閉折線,並且每個線節與規定的球交於兩個點,而折線的所有頂點在球外,這些點分折線為3n個線段。已知,毗鄰頂點A
1的線段彼此相等,同樣的條件對於頂點
也是對的,證明:對毗鄰頂點A
n的線段彼此也相等。
提示 毗鄰頂點Ai的線段相等,其中i=1,2,...,n-1,根據由一點引的割線段乘積的定理,位於球內部的這些線節上的線段也彼此相等。因此,位於球內部的所有線段彼此相等,因為對相鄰的頂點這些線段中的一個是共同的。所以它們等於對頂點An的線節,但此時根據同一個定理對毗鄰頂點An這些線節的線段也彼此相等。
7.已知四條直線,它們中的任三條不平行於一個平面,證明:存在空間四邊形,它的邊平行於這些直線,同時平行於對應直線的邊的比,對所有這樣的四邊形是相同的。
提示 設a,b,c和d是平行於已知直線的向量,因為在空間的不在一個
平面上的任意三個向量形成基底,那么存在這樣的非零數a,β和γ,使得αa+βb+γc+d=0。向量αa、βb、γc、d是所求四邊形的邊。設α1a、β1b、γ1c、d是另一個這樣的四邊形的邊的向量,則αa+βb+γc+d=0=α1a+β1b+γ1c+d,即(α1-α)a+(β1-β)b+(γ1-γ)c=0,因為向量a, b和c不在一個平面上,所以α=α1,β=β1和γ=γ1。
 圖1
圖1 圖2
圖2