基本介紹
- 中文名:矢量磁位
- 外文名:vector magnetic potential; magnetic vector potential
- 所屬領域:電力術語
磁矢勢,求解三維準靜態矢量磁位的快速多極方法,積分方程的離散,靜電模擬,示例計算,結論與下一步工作,
磁矢勢
直觀而言,磁矢勢似乎不及磁場來得“自然”、“基本”,而在一般電磁學教科書亦多以磁場來定義磁矢勢。以前,很多學者認為磁矢勢並沒有實際意義,只是人為的物理量,除了方便計算以外,別無其它用途。但是,詹姆斯·麥克斯韋頗不以為然,他認為磁矢勢可以詮釋為“每單位電荷儲存的動量”,就好像電勢被詮釋為“每單位電荷儲存的能量”。相關論述,稍後會有更詳盡解釋。
磁矢勢的數值是相對的,相對於某設定數值。因此,學者會疑問到底儲存了多少動量?不論如何,磁矢勢確實具有實際意義。尤其是在量子力學里,於1959年,阿哈諾夫-波姆效應闡明,假設一個帶電粒子移動經過某零電場、零磁場、非零磁矢勢場區域,則此帶電粒子的波函式相位會有所改變,因而導致可觀測到的干涉現象 。越來越多學者認為電勢和磁矢勢比電場和磁場更基本。不單如此,有學者認為,甚至在經典電磁學里,磁矢勢也具有明確的意義和直接的測量值。
磁矢勢與電勢可以共同用來設定電場與磁場。許多電磁學的方程可以以電場與磁場寫出,或者以磁矢勢與電勢寫出。較高深的理論,像量子力學理論,偏好使用的是磁矢勢與電勢,而不是電場與磁場。因為,在這些學術領域裡所使用的拉格朗日量或哈密頓量,都是以磁矢勢與電勢表達,而不是以電場與磁場表達。
求解三維準靜態矢量磁位的快速多極方法
近年來 ,快速多極方法(FMM)算法越來越多地套用於電磁場數值計算的各個領域 ,與傳統的算法比較, 套用 FMM 算法來求解大尺寸電磁散射問題 ,可大大降低記憶體需要, 計算速度顯著提高。FMM算法與邊界元和有限元方法相結合, 來求解大型渦流場問題也取得了很好的計算效果。由於 FMM算法很適合於進行並行計算 ,採用並行 FMM 算法可以求解上百萬個未知數的大型矩陣向量乘法運算。 大量的數值計算試驗已經證明了 FMM 算法是一種非常有效的數值加速算法。
在積體電路互連線的分析與設計過程中, 需要計算互連線在空間中某些區域內的電磁場分布 , 在這種情況下,套用有限元方法求解電磁場問題需要對整個場域進行剖分。 由於積體電路互連線分布結構複雜,為獲得較高的精度需要加密對場域或邊界的剖分,這樣計算機的記憶體占用和計算時間會急劇增加.。首先根據計算精度的要求把連續分布的場源進行離散化處理 ,然後通過靜電類比分析,將求解三維準靜態矢量磁位的問題轉化為多體問題 ,進而利用快速多極方法來計算。該算法只需要對場源和需要計算的場域進行剖分, 大大降低了對計算機記憶體的要求, 提高了計算速度。通過對積分方程的離散和靜電類比分析 ,推導出了套用多極加速方法計算磁矢位的公式 , 最後通過算例證明了算法的正確性和有效性。
積分方程的離散
根據電磁場數值分析理論 ,在研究連續分布的量的作用時,可以把它近似看成離散分布的量 ,考察其單個離散元的作用 ,如果問題是線性的,那么通過疊加的辦法就能求得整體的效果。 對於各向同性媒質中的載流導體 ,電流密度矢量為 ,在無限大空間中產生的磁矢位為
,在無限大空間中產生的磁矢位為

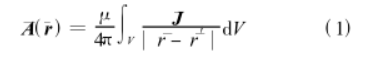 公式(1)
公式(1)根據計算精度的要求 ,首先將導體剖分為 N個小體積單元,可以近似認為每個小體積單元內的電流密度為恆定, 經過這樣的離散化 ,得到
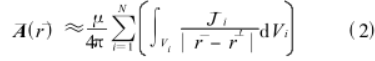 公式(2)
公式(2)在直角坐標系下 ,把電流密度矢量 分解為 3 個方向上的分量
分解為 3 個方向上的分量

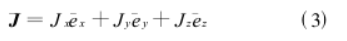 公式(3)
公式(3)那么
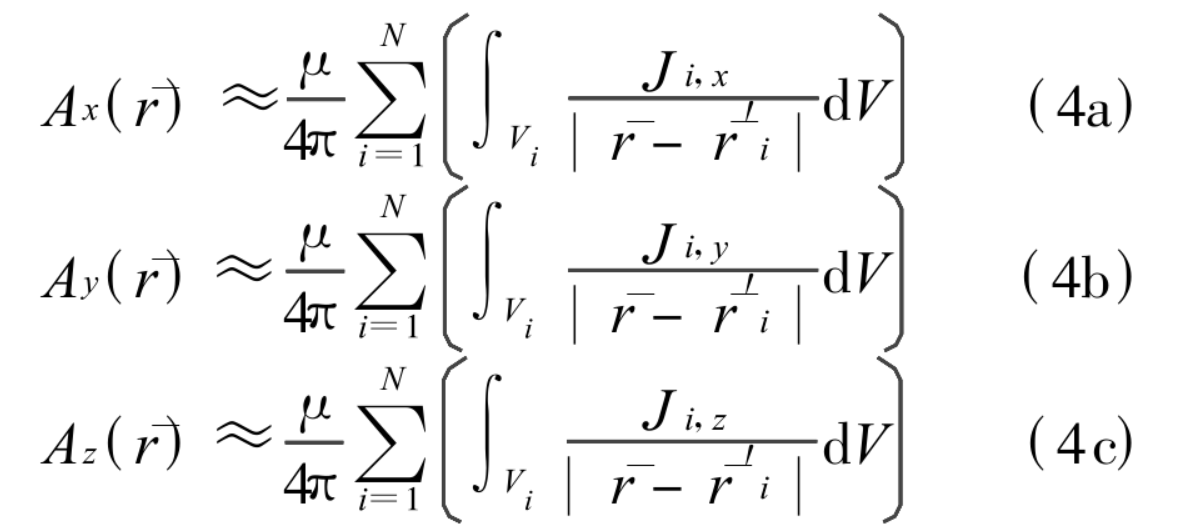 公式(4)
公式(4)式中 : 、
、 、
、 表示剖分單元i的電流密度
表示剖分單元i的電流密度 在x、y、z方向上的分量。矢量磁位
在x、y、z方向上的分量。矢量磁位 由三個方向的分量合成
由三個方向的分量合成





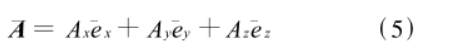 公式(5)
公式(5)靜電模擬
設空間中體積單元 處分布著體電荷密度為
處分布著體電荷密度為 的靜止電荷 ,在空間中 P點處產生的電位
的靜止電荷 ,在空間中 P點處產生的電位


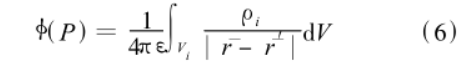 公式(6)
公式(6)因為體積單元 很小, 從而體積單元內的電荷密度
很小, 從而體積單元內的電荷密度 可近似為恆定。 根據 FMM 算法中多極展開的思想,當計算遠場區域的電位時,我們可以進一步用體積單元內均勻分布的 M 個等量靜止電荷來近似電荷的體分布
可近似為恆定。 根據 FMM 算法中多極展開的思想,當計算遠場區域的電位時,我們可以進一步用體積單元內均勻分布的 M 個等量靜止電荷來近似電荷的體分布


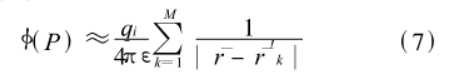 公式(7)
公式(7)M個靜止電荷帶電量相等,其電量為

比較(4)、(6)和(7)可以得到
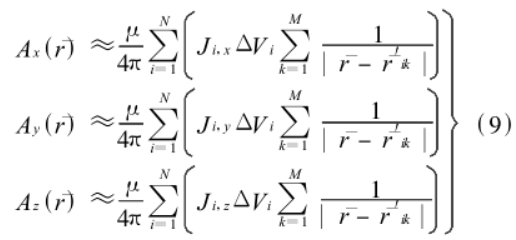 公式(9)
公式(9)式中: 表示剖分單元i 的體積.。由式(9)可見 ,經過積分方程離散和靜電模擬分析, 我們已經把求解載流導體在無限大空間中產生的磁矢位的問題轉化為多體問題, 這樣經過 3 次運用 FMM 算法, 分別求出
表示剖分單元i 的體積.。由式(9)可見 ,經過積分方程離散和靜電模擬分析, 我們已經把求解載流導體在無限大空間中產生的磁矢位的問題轉化為多體問題, 這樣經過 3 次運用 FMM 算法, 分別求出 、
、 和
和 , 套用式(5)最後合成磁矢位
, 套用式(5)最後合成磁矢位 。
。





示例計算
例 1:如圖 1 所示 ,求載流導體 A 在其自身所在空間區域和導體 B 所在的空間區域的矢量磁位。載流導體 A 電流分布均勻, 電流密度就為 =0.0001A/μm2。
=0.0001A/μm2。

首先對載流導體 A 和 B 進行剖分,取剖分單元為立方體,分別採取 3 種不同的剖分密度計算, 即分別取體積單元的邊長 =0.5μm ,
=0.5μm , =0.25 μm,
=0.25 μm, =0.125 μm ,取每個體積單元的等效靜止電荷數M =8。套用 FMM 算法求解時 ,剖分場域層數為 5,多極展開截止級數項 p=12。
=0.125 μm ,取每個體積單元的等效靜止電荷數M =8。套用 FMM 算法求解時 ,剖分場域層數為 5,多極展開截止級數項 p=12。



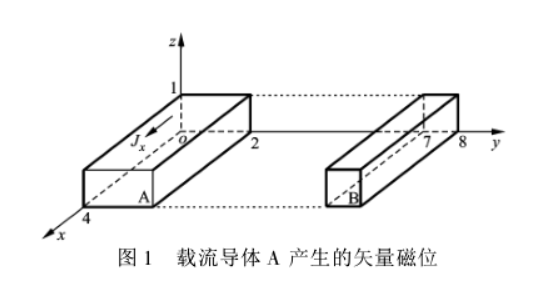 圖1
圖1分別採取不同剖分密度計算導體 A 、B 所在空間區域中部分場點的矢量磁位, 計算結果見表 1、表
2。表中 、
、 和
和 分別表示 3 種不同剖分密度下套用多極算法計算的矢量磁位。
分別表示 3 種不同剖分密度下套用多極算法計算的矢量磁位。 為利用兩點之
為利用兩點之




間的距離公式直接計算的結果, 其剖分密度為 a =0.025 μm ,將 作為準精確值與多極算法的計算
作為準精確值與多極算法的計算

結果進行比較。


 表1和表2
表1和表2FMM 計算結果與的相對誤差為 。
。













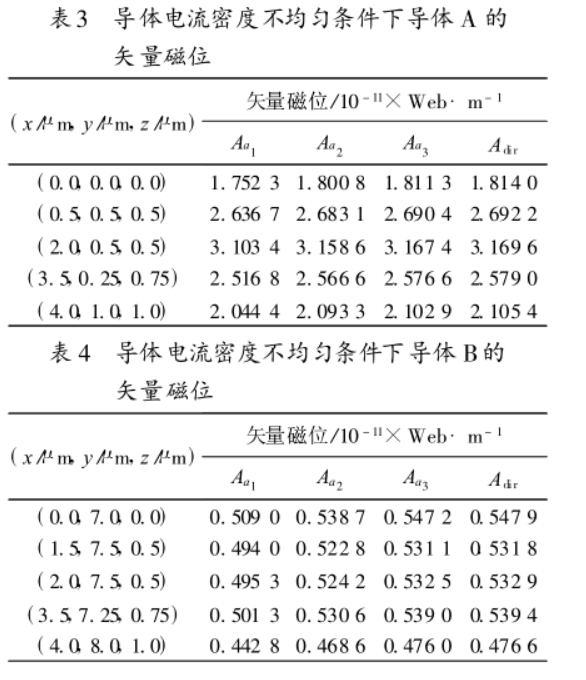 表3和表4
表3和表4


以上兩個例子可以證明, 經過積分方程離散和模擬分析, 套用 FMM 算法可正確地計算三維空間載流導體的矢量磁位, 計算誤差可通過剖分密度進行控制。由多極算法的加速理論可知,當計算的粒子數很大時 ,該算法的加速性能將會得到很好的體現。
結論與下一步工作
通過積分方程離散和靜電類比分析, 將求解準靜態電磁場矢量磁位的問題轉化為多體問題 ,利用 FMM 算法進行求解。提出的方法擴展了FMM 算法在準靜態電磁場矢量磁位數值計算領域中的套用 ,下一步的工作將該算法用於片上互連線電感參數的計算 , 為快速提取互連線寄生參數尋找快速可行的算法。