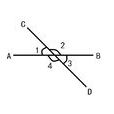
定義
有唯一公共點的兩條直線叫作相交線。
補角和對頂角
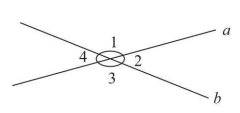 圖1
圖1(1)
鄰補角:∠1和∠2有一條公共邊.它們的另一邊互為反向延長線(∠1和∠2互補),具有這種關係的兩個角,互為鄰補角。如:∠1和∠4,∠2和∠3等。
(2)
對頂角:∠1和∠3有一個公共頂點,並且∠1的兩邊分別是∠3的兩邊的反向延長線,具有這種位置關係的兩個角,互為對頂角。如:∠2和∠4。
對頂角的性質:對頂角相等
關鍵提醒: ①鄰補角是有特殊位置關係的兩個互補的角,要注意區別
補角與鄰補角這兩個概念,互為補角的兩個角只強調數量關係,不強調位置關係;鄰補角不僅強調數量關係,同時也強調位置關係。
②對頂角和鄰補角是成對出現的,只有當兩條直線相交時,才產生對項角和鄰補角。
垂線
(1)
垂直:兩條直線相交所成的四個角中,有一個角為90°時,稱這兩條直線互相垂直。
(2)
垂線:兩條直線互相垂直,其中的一條直線叫作另一條直線的垂線,交點叫作垂足。
(3) 性質:①過一點有且只有一條直線與已知直線垂直;②連線直線外一點與直線上各點的所有線段中,垂線段最短,簡單說成:垂線段最短。
關鍵提醒: ①對於垂線的性質,必須強調“在同一平面內”,否則,在空間裡,經過一點與已知直線垂直的直線有無數條;②“過一點”包括直線上一點和直線外一點,“有”表示存在,“只有”表示唯一。
(4) 點到直線的距離:直線外一點到這條直線的垂線段的長度,叫作點到直線的距離。
關鍵提醒: 垂線是直線,垂線段特指一條線段,點到直線的距離是指垂線段的長度,是一個數量,是有單位的。
例題 如圖2所示,直線AB,CD相交於點0,射線OM平分∠AOC,ON⊥OM,若∠AOM=35°,則∠CON的度數為( )。
A.35° B.45° C.55° D.65°
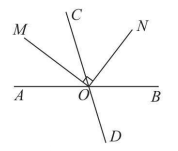 圖2
圖2解析:因為
射線OM平分∠AOC,∠AOM=35°,所以∠MOC=35°,因為ON⊥OM,所以∠MON=90°,所以∠CON=∠MON-∠MOC=90°-35°=55°。
答案:C
各角信息
三者位置特點、圖形特徵見表1。
角的名稱 | 位置特點 | 圖形特徵 |
同位角 | 在兩條被截直線的同旁,在截線同側 | 形如字母“F”,如圖3 |
內錯角 | 在兩條被截直線的內部,在截線兩側 | 形如字母“Z”,如圖4 |
同旁內角 | 在兩條被截直線的內部,在截線同側 | 形如字母“n”,如圖5 |
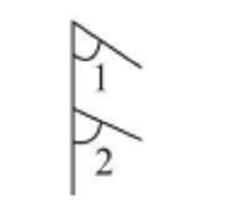 圖3
圖3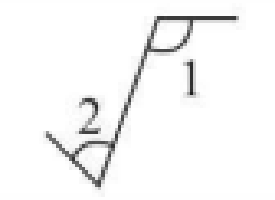 圖4
圖4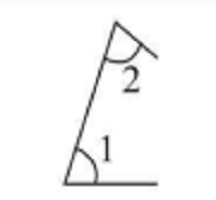 圖5
圖5
 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4 圖5
圖5