無贅集(irredundant set)是圖論的一個重要概念，指圖的節點集的一種子集，不是別的無贅集的真子集的無贅集稱為極大無贅集。
基本介紹
- 中文名：無贅集
- 外文名：irredundant set
- 所屬學科：數學
- 所屬問題：組合學(圖與超圖)
- 簡介：圖的節點集的一種子集
基本介紹,相關概念及性質,
基本介紹
定義1 設
為一個圖，且
，如果對每個
，存在一點
，使得
，則稱S為G的一個無贅集。容量最大的無贅集稱為最大無贅集。最大無贅集包含的點數稱為(上)無贅數(the upper irredundancenumber)，記為
。
定義2 若S為G的一個無贅集，且對於
均不是G的無贅集，則稱S為G的一個極大無贅集。
當然，最大的極大無贅集的容量為G的上無贅數，記為 。最小的極大無贅集的容量稱為G的(下)無贅數(the lower irredundance number)，記為
。
即有
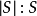
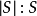
相關概念及性質
定義3 設D為圖G的一個控制集，如果對於每一個
均不是G的控制集，則稱D為圖G的一個極小控制集。最大的極小控制集的容量稱為圖G上控制數(the upper domination number)，用
表示。即有
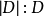
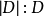
由上述定義可見，
對任何圖G均成立。值得注意的是，對於一個給定的圖，一般來說，其極小控制集與最小控制集不同。最小控制集雖然不是唯一的，但其所有的最小控制集包含的點數是唯一確定的，即其控制數。但極小控制集就不同了，不同的極小控制集可能包含不同數目的點數。取遍圖的所有極小控制集，容量最大者包含的點數為上控制數，容量最小者包含的點數為控制數。
當然，一個圖的最小控制集必為極小控制集，但反之不然。一個圖的上控制數與控制數之間並沒有必然聯繫。
定義4 設
為一個圖，且
，如果S中任何兩點在G中都是不鄰的，則稱S為G的一個獨立集。在一個圖的所有獨立集中，容量最大的獨立集稱為最大獨立集。最大獨立集所包含的點數稱為獨立數(independent number)，用
(或者
)表示。
由定義不難看出，圖G的最大獨立集均為G的極小控制集，從而有以下結論：
引理1 對任何圖G，均有
定義5 設S為G的一個獨立集，若對於
均不是G的獨立集，則稱S為G的一個極大獨立集。
當然，最大的極大獨立集的容量為G的獨立數。最小的極大獨立集的容量稱為G的下獨立數或獨立控制數，記為i(G)。即有
由定義可見，圖G每個極大獨立集均為圖G的控制集，從而有以下結論：
引理2 對任何圖G，均有
同樣值得注意的是，對於一個給定的圖G，一般來說，其極大獨立集與最大獨立集不同。最大獨立集雖然不是唯一的，但其所有的最大獨立集包含的點數是唯一確定的，即圖的獨立數。但極大獨立集就不同了，不同的極大獨立集可能包含不同數目的點數。取遍圖的所有極大獨立集，容量最大者包含的點數為獨立數，容量最小者包含的點數為下獨立數i(G)。
由定義1,2可見，一個圖G的每個最大獨立集均為G的一個無贅集，這表明
