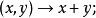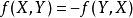正交幾何(orthogonal geometry)是一種向量空間的幾何，即關於非退化對稱雙線性型的向量空間的研究。這裡的對稱雙線性型B是指對任意向量x，y有B(x，y)=B(y，x)的雙線性型。對有限維空間中取定的一組基{e1，e2，…，en}，當基域的特徵不為2時，對稱雙線性型B的矩陣S=(B(ei，ej))滿足S′=S，即為對稱矩陣。
基本介紹
- 中文名：正交幾何
- 外文名：orthogonal geometry
- 領域：數學
- 學科：幾何學
- 研究對象：非退化對稱雙線性型的向量空間
- 矩陣：對稱矩陣
概念,幾何學,向量空間,對稱雙線性型,
概念
正交幾何是一種向量空間的幾何，即關於非退化對稱雙線性型的向量空間的研究。這裡的對稱雙線性型B是指對任意向量x，y有B(x，y)=B(y，x)的雙線性型。對有限維空間中取定的一組基{e1，e2，…，en}，當基域的特徵不為2時，對稱雙線性型B的矩陣S=(B(ei，ej))滿足S′=S，即為對稱矩陣。設P是Vn(Fq)的m維子空間，代表該子空間的一個秩為m的m×n矩陣也用P表示。當q為奇數且S為非奇異對稱矩陣時，若PSP′=0，則稱P為全迷向子空間；若PSP′非奇異，則稱P為非迷向子空間。利用正交幾何中不同類型的子空間，可以構作結合方案及PBIBD設計。例如，當n≥4時取奇數特徵有限域上n維正交幾何中1維迷向子空間的全體作為處理的集合，兩個1維迷向子空間，若生成一個2維全迷向子空間，則規定它們有第一種結合關係，否則它們有第二種結合關係，這樣便得到一個結合方案。利用該結合方案可構作PBIBD設計，比如取m維作迷向子空間作為區組，並規定關聯關係由子空間之間的包含關係決定。
幾何學
研究圖形性質的一門數學分支。
“geometry”來自拉丁文geometria，原意是土地測量。古埃及的幾何學，起源於尼羅河泛濫後對土地所進行的重新測量。古巴比倫人已經知道了一些圖形面積與體積的求法;還知道圓周長與直徑的比為定值。
古希臘的歐幾里得，把前人的幾何知識(幾何證明與抽象概念等)系統化，整理成嚴密的演繹系統，寫出了《幾何原本》。這本書問世後，幾何學在數學中曾長期占主導地位。直到17世紀初，代數學得到發展以後，幾何學在數學中所處的主導地位才被代數學取代。而用代數方法研究幾何問題，又導致了解析幾何學的產生。在18、19世紀，由於力學、工程、測量等方面的需要，產生了畫法幾何學、射影幾何學和微分幾何學。而對歐氏第五公設的研究、又導致非歐幾何學的產生。幾何學的各個分支，可以定義為研究特定圖形在特定的變換下的不變性質。
我國在很早就已出現論證幾何學的萌芽。在公元前5世紀墨子所著的《墨經》中，有豐富且嚴謹的幾何方面的論述。其中所涉及的幾何內容，與歐幾里得的《幾何原本》大致相同，而且其中的定義，與現行中學幾何教科書基本相同。此外，其中還有一系列理論性的命題，反映出墨家重視抽象性及邏輯嚴密性的新思想和新嘗試。可惜，後來未能形成為嚴密的演繹體系。
20世紀以來，由於現代物理、現代工程技術的發展，又促進了微分幾何學與計算幾何學的發展。在現代，幾何學泛指對由公理所規定性質之集合進行研究的學科。皮亞諾與希爾伯特，對歐氏幾何學的現代化起過重要的作用。
“幾何”是《幾何原本》1607年的中譯本中開始使用的譯名，它的原意指“多少”或“大小”。“幾何”是意譯，並不是音意並譯。
向量空間
設K為交換體，稱賦以由下列兩個給定法則所定義的代數結構的集合E為K上的向量空間：
這兩個法則滿足下列條件：
a)賦以加法的集合E是交換群;
b) 對K的任一元素偶(α，β)，以及對E的任一元素x，α(βx)=(αβ)x;
c) 對E的任一向量x，1x=x，其中1表示體K的單位元素;
d)對K的任一元素偶(α，β)，以及對E的任一元素偶(x，y)，
(α+β)x=αx+βx
α(x+y)=αx+αy.
當體K不再假定為交換的時，滿足上述條件的集合E稱為K上的左向量空間。
如果條件α(βx)=(αβ)x換為α(βx)=(βα)x，則稱E為K上的右向量空間。
對稱雙線性型
對稱雙線性型(symmetric bilinear form)是線性空間V上的雙線性型f(α，β)，如滿足：對所有α，β∈V，都有f(α，β)=f(β，α)，則稱f(α，β)為對稱雙線性型。在V中取定一個基ε1，ε2，…，εn，令α=x1ε1+x2ε2+…+xnεn，則f(α，α)為關於變數組x1，x2，...，xn的二次型。數域P上任一二次型都可用此法由對稱雙線性型得出。
定義1設f是V上的雙線性型，若對V中任意向量X、Y有
，則稱f是V上的對稱雙線性型。
明顯地，f是對稱雙線性型的充要條件是，f的矩陣是對稱的。
定義2設f是V上的雙線性型，若對V中任意向量X，Y有
，則稱f是V上的反對稱雙線性型。
同樣有，f是反對稱雙線性型的充要條件是，f的矩陣是反對稱的。顯然，V上的一個任意的雙線性型都可以表示成對稱的和反對稱的雙線性型的和，而且，這種表示法是惟一的。
