基本介紹
- 中文名:歐拉圖
- 外文名:Euler Graph
- 發明者:歐拉
- 實質:具有歐拉迴路的圖
- 半歐拉圖:具有歐拉通路而無歐拉迴路的圖
- 起源:18世紀
- 現代擴展:蜘蛛圖
起源歷史
 圖1.哥尼斯堡七橋問題
圖1.哥尼斯堡七橋問題歐拉環遊
弗勒里算法
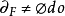


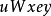
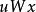
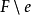
相關定理
 圖2.
圖2.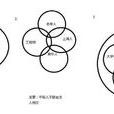
 圖1.哥尼斯堡七橋問題
圖1.哥尼斯堡七橋問題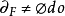


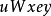
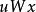
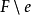
 圖2.
圖2.歐拉圖是指通過圖(無向圖或有向圖)中所有邊且每邊僅通過一次通路,相應的迴路稱為歐拉迴路。具有歐拉迴路的圖稱為歐拉圖(Euler Graph),具有歐拉通路而無歐拉迴路...
歐拉圖解法又稱歐拉邏輯圖解法, 是一種邏輯學上的圖解,用來揭露兩個概念是否有重疊關係。...
《歐拉圖與相關專題》是迄今為止唯一的一本全面闡述歐拉圖理論的主要研究成果和研究方法及其與其他圖論問題之間的聯繫的專著。...
如果圖G中的一個路徑包括每個邊恰好一次,則該路徑稱為歐拉路徑(Euler path)。如果一個迴路是歐拉路徑,則稱為歐拉迴路(Euler circuit)。具有歐拉迴路的圖稱為歐拉...
歐拉路徑,無向連通圖中的一條路徑。...... 具有歐拉路徑但不具有歐拉迴路的圖稱“半歐拉圖”。找出歐拉迴路或歐拉路徑可採用深度優先搜尋。 [1] ...
歐拉有向圖(Eulerian digraph)一種特殊的強連通有向圖.若一個有向圖D上存在一條有向閉徑C,使得D的每一條弧都在C上,則稱D為歐拉有向圖.這種閉徑被稱為有...
介紹 歐拉跡(Eulerian trail)圖論術語.指圖的一條通過圖中每條邊恰好一次的途徑.圖的一條閉歐拉跡稱為該圖的歐拉環遊.含有歐拉環遊的圖稱為歐拉圖.歐拉(Eider,...
在數學及許多分支中都可以見到很多以歐拉命名的常數、公式和定理。在數論中,歐拉定理(Euler Theorem,也稱費馬-歐拉定理或歐拉函式定理)是一個關於同餘的性質。歐拉...
歐拉的圖論貢獻:連通圖 (connected graph) ,生成樹 (spanning tree) 以及相關證明、歸納...
先定義能一筆畫出並回到起點的圖為歐拉圖,連通就是說任意兩個節點之間可以找到一條連線它們的線。這個要求看來很重要,直觀方法中與這一點對應的是說原圖本身不能...
范更華,男,1957年2月出生於福建福鼎,祖籍福建壽寧。曾任中共福州大學委員會常委,副校長,教授,博士生導師。主要從事圖論領域中的結構圖論、極圖理論、帶權圖、歐拉...
