歐氏環(Euclid ring)比主理想整環更窄的環類.它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R0=R-{ 0 }到非負整數集內的一個映射適合條件:任給非零元a,對R中任意元b,恆有q,r屬於R,使得b=qa+r,其中r=0或φ(r)<φ(a),則稱R為歐氏環.整數環、域上一元多項式環都是歐氏環.
基本介紹
- 中文名:歐氏環
- 外文名:Eucild Ring
- 學科:近世代數,抽象代數
- 領域:數學
定義










相關定理











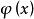
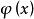

























例子




歐氏環(Euclid ring)比主理想整環更窄的環類.它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R0=R-{ 0 }到非負整數集內的一個映射適合條件:任給非零元a,對R中任意元b,恆有q,r屬於R,使得b=qa+r,其中r=0或φ(r)<φ(a),則稱R為歐氏環.整數環、域上一元多項式環都是歐氏環.





















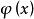
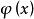





























歐氏環(Euclid ring)比主理想整環更窄的環類.它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R0=R-{ 0 }到非負整數集內的一個...
歐式風格,是一種來自於歐羅巴洲的風格。主要有法式風格,義大利風格,西班牙風格,英式風格,地中海風格,北歐風格等幾大流派。所謂風格,是一種長久以來隨著文化的潮流...
現代歐式風格,分為幾種類型:文藝復興式、巴洛克式、洛可可式或美國殖民地式等。但是他們的主要構成方法是一樣的,基本上有三類,一類是室內構件要素,例如拱門、柱式...
歐式構件,又名GRC歐式裝飾構件。GRC是Glass Fiber Reinforced Cement(水泥增強玻璃纖維)的英文縮寫,是國外七十年代發明並廣泛套用的一種複合材料。它是由快硬矽酸鹽...
《歐式新古典(英漢對照)》講述新古典主義設計在建築上具有卓越的影響力,這可以追溯到古希臘和古羅馬時期。雅典的帕台農神廟和羅馬的萬神廟都蘊含著這一形式的元素...
歐式田園風格,重在對自然的表現,但不同的田園有不同的自然,進而也衍生出多種風格,中式的、歐式的,甚至還有南亞的田園風情,各有各的特色,各有各的美麗。歐式...
古典歐式風格是追求華麗、高雅的古典,設計風格直接對歐洲建築、家具、繪畫、文學甚至音樂藝術產生了極其重大的影響,具體可以分為六種風格來簡述:羅馬風格、哥德式風格...
概述歐式光波離子包皮包莖手術是一種完全符合生殖衛生及疾病預防、保健的手術,包皮環切術切除過長的包皮不僅有益於陰莖的正常發育,而且可以防止包皮垢的積聚,有效預防...
歐式變電站最早是由歐洲引進中國的一項變電技術,也叫YBW-12系列預裝式變電站。YBW-12系列預裝式變電站,是將高壓電器設備、變壓器、低壓電器設備等組合成緊湊型成套...
歐式線條也稱EPS線條是我國建築裝飾工程引進新型材料,關於歐式線條就不得不提到歐式建築,歐式風格建築強調以華麗的裝飾、濃烈的色彩、精美的造型達到雍容華貴的裝飾效果...
歐式護欄網(Palisade)也稱為歐式護欄(palisade fence)在國內也許不知道,而在國外早已被人們所熟知,它的到來替代了過去的大磚牆和一些粗笨的護欄網,使您的生活環境...
歐式家具是歐式風格裝修的家具,以義大利、法國、英國和西班牙風格的家具為主要代表。講究手工精細的裁切雕刻。其中,歐式家具以手工雕刻見長,法國和義大利是世界範圍內...
歐式燈,奢華典雅的代名詞。源自歐洲古典風格藝術,仿歐洲古宮庭式效果。歐式古典的魅力,在於其獨具歷史歲月的痕跡,其體現出的優雅雋永的氣度代表了主人的一種卓越的...
歐式家居風格以華麗的裝飾、濃烈的色彩、精美的造型達到雍容華貴的裝飾效果。美麗大方。典雅...
歐式黃金市場主要在倫敦黃金市場和蘇黎士黃金市場這類黃金市場裏的黃金交易沒有一個固定的場所。在倫敦黃金市場,整個市場是由各大金商、下屬公司之間的相互聯繫組成,...
該技術是南京454院生殖整形專家聯合軍內數百位軍內生殖醫學外科整形專家,將歐式、美式、韓式、中式商環技術包皮整形所有技術特色優勢,以及國際先進的歐洲雷射離子技術,...
歐式箱變的高壓室一般是由高壓負荷開關、高壓熔斷器和避雷器等組成的,可以進行停送電操作並且有過負荷和短路保護。低壓室由低壓空氣開關、電流互感器、電流表、電壓...
歐式變壓器也稱歐式變電站,是箱變的其中一種。它具有成套性強、體積小、結構緊湊、運行安全可靠、維護方便、以及可移動等特點。...
歐式起重機的概念是近些年行業內形成的,目的是區別於以往的所謂國產、蘇(蘇聯)式、傳統式起重機。主要包含:橋式起重機,門式起重機,懸臂吊,柔性梁起重機,防爆起重...
修道院建築面南向,面積5600多平方米,為左右對稱分布的建築群,平面呈倒“凹”形,由教堂和歐式環樓組成。中文名稱 嘉興文生修道院 地理位置 浙江省嘉興市南湖區 ...
