基本介紹
- 中文名:機率測度
- 外文名:probability measure
- 學科:數學
- 本質:機率空間一組事件的實值函式
- 性質:加和性
- 相關名詞:勒貝格測度
簡介
定義



示例套用
延伸
勒貝格測度





博雷爾測度















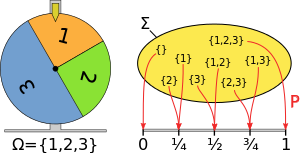
機率測度(probability measure)是機率論、遍歷理論等數學分支中常用的一種重要的有限測度。在數學中,機率測度是在滿足測度屬性(如可加性)的機率空間中的一組事件上...
《機率與測度》是2007年世界圖書出版公司出版的圖書,作者是別林斯里。該書主要內容包括機率、測度、積分、隨機變數及數學期望、分布的收斂的問題、導數與條件期望、...
測度論是研究一般集合上的測度和積分的理論。它是勒貝格測度和勒貝格積分理論的進一步抽象和發展,又稱為抽象測度論或抽象積分論,是現代分析數學中重要工具之一。 ...
數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的,後來人們希望把積分...
《機率與測度論》是2007年人民郵電出版社出版的圖書,作者是RobertB.Ash。...... 《機率與測度論》是2007年人民郵電出版社出版的圖書,作者是RobertB.Ash。...
機率分布,是指用於表述隨機變數取值的機率規律。事件的機率表示了一次試驗中某一個結果發生的可能性大小。若要全面了解試驗,則必須知道試驗的全部可能結果及各種可能...
機率測度半群(semigroup of probability mea-sure)一種特殊的半群.指由定義在緊緻半群上所有機率測度所構成的半群.設S是緊緻半群,P(S>是S上所有機率測度的...
機率論,是研究隨機現象數量規律的數學分支。隨機現象是相對於決定性現象而言的,在一定條件下必然發生某一結果的現象稱為決定性現象。例如在標準大氣壓下,純水加熱到...
δ測度是測度論中的一個概念。給定一個δ-代數 ,以及其上的一個測度 ,如果該測度是一個有限的實數(而不是無窮大),那么就稱這個測度為有限測度。如果 能夠表示...
S測度是超實數集*R中的一種測度,是魯賓孫(Robinson,A.)於20世紀60年代初引入的。...... 積分推廣到任意的集合上,就發展出測度的概念,它在數學分析和機率論有...
維納測度是定義在連續函式空間上的一種描述布朗運動的測度。維納測度也叫維納過程。在數學中,維納過程是一個連續的時間隨機過程,以諾伯特·維納命名。它通常被稱為...
測度代數(measure algebra)定義了正測度的σ代數,若F既是代數又是測度環,則稱F是一個測度代數。若測度μ是有限的或σ有限的,則稱相應的測度代數(測度環)為有限...
吉布斯測度(Gibbs measure)是一種常用的測度。數學上,測度是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。...
機率分析又稱風險分析,是通過研究各種不確定性因素髮生不同變動幅度的機率分布及其對項目經濟效益指標的影響,對項目可行性和風險性以及方案優劣作出判斷的一種不確定...
零測度就是某個集合的測度為0。數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。...
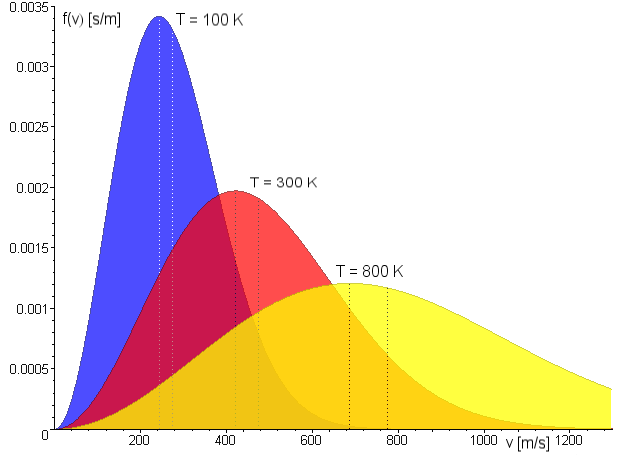
在數學中,連續型隨機變數的機率密度函式(在不至於混淆時可以簡稱為密度函式)是一個描述這個隨機變數的輸出值,在某個確定的取值點附近的可能性的函式。而隨機變數的...
