模格

模格(modular lattice)亦稱戴德金格，是格論中僅次於分配格的一類重要格，設L是格，對任意a，b，c∈L，若L滿足下列條件之一：L5：若a≤c，則a∨(b∧c)=(a∨b)∧c；L5′：(a∧b)∨(a∧c)=a∧(b∨(a∧c))；則稱L為模格，L5稱為模恆等式。分配格是模格。群的正規子群格、環的理想格都是模格。格L是模格若且唯若L不含五邊形格。科里比亞(M.Kolibiar)於1956年用兩個恆等式(x∨(y∧y))∧y=y和((x∧y)∧z)∨(x∧t)=((t∧x)∨(z∧y))∧x刻畫了模格，模格中一個非常重要的定理是戴德金的轉置原理：若L是模格，a，b∈L，則φ_b：x→x∧b是[a，a∨b]到[a∧b，b]的同構，其逆同構為ψ_a：y→y∨a.從而在模格L中，若x，y∈[a∧b，b]⊆L，則a ∨(x∧y)=(a∨x)∧(a∨y)。

基本介紹

• 中文名：模格
• 外文名：modular lattice
• 所屬學科：數學
• 所屬問題：離散數學（組合序）
• 別稱：戴德金格
• 簡介：格論中僅次於分配格的一類重要格

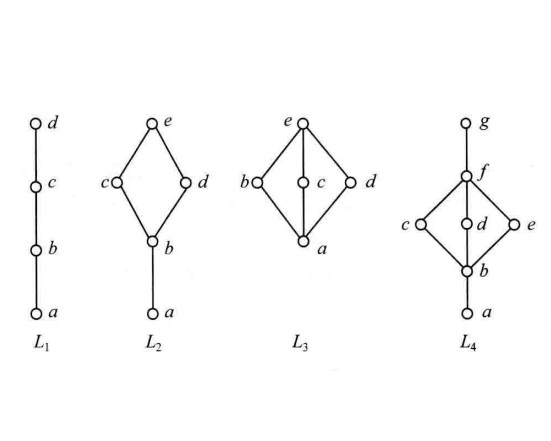
總體介紹

模格是一種組合構形，是滿足如下條件的格：對於格的任意元素x，y和z，若x≤z，則x∨(y∧z)=(x∨y)∧z。

因此，模格是把滿足分配律的要求僅局限在可比較元素之間，從而模格可視為分配格的推廣，一個格是分配格，則必為模格。

圖1里，M₅，N₅均不是分配格，但M₅是模格，而N₅不是模格。

圖1

在模格L上，映射φ_a把x映照為x∧a；映射ψ_b則把y映照為y∨b，這裡a和b均為L的固定的元素，於是φ_a和ψ_b為區間[b，a∨b]和[a∧b，a]之間互逆的同構映射，因而這兩個區間是同構的。模格的這一基本性質，亦可作為模格的另一等價定義。

在模格上，把形如I₁=[a∧b，a]，I₂=[b，a∨b]的區間稱為傳遞區間，若在兩區間[x，y]和[x′，y′]之間存在一組區間I₁，I₂，…，I_k，使得相鄰兩個區間都是傳遞區間，而且I₁=[x，y]，I_k=[x′，y′]，則稱[x，y]和[x′，y′]中一個為另一個的投影區間。模格的投影區間均是同構的，這種結構上的均勻性是模格的主要特性。

模格也可由模元素來定義：格L為模格，若且唯若L的所有元素均為模元素，若L的元素a滿足：對於L的任意元素x，y，由x≤y得到x∧(a∨y)=(x∧a)∨y，則稱a為模元素，此外，格L上的一對元素a和b，若對於L的所有元素z它們滿足：若b≥z，則有b∧(a∨z)=(b∧a)∨z，此時稱a，b為模元素對，由定義知，在模元素對a和b之間是有序關係的，這就是說，當a和b為模元素對時，b和a不一定為模元素對，因此，一般把模元素對a和b記為二元序對(a，b)_M，或aMb。模格亦可由模元素對刻畫：格L為模格，若且唯若L的每對元素均為模元素對，關於模元素對的序關係為對稱的格，即若a和b為模元素對，則b和a也為模元素對，相應的格稱為模對稱格。

例題解析

例1 設S是一個集合，則S的冪集格(P(S)，⊆)是一個模格。因為對於任意的A，B，C∈P(S)，當B⊆A時，利用集合論中交對於並的分配律有：

A∩(B∪C)=(A∩B)∪(A∩C)=B∪(A∩C)。

例2 圖2給出了五個格，不難驗證和L₄都是模格。但L₅不是模格，這是因為由c≼d，可得d∧(c∨b)=d，c∨(d∧b)=c，但d≠c。我們稱L₃為鑽石格，L₅為五角格。

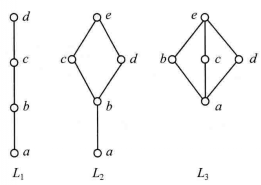圖2（a）

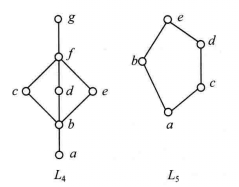圖2（b）

例2中的五角格是很重要的，可利用它來判斷一個格是不是模格。

定理 一個格S是模格，若且唯若S中不含有與五角格同構的子格。

該定理的證明比較複雜，在這裡略去，只要會利用即可。

例3 如圖3所示的格S中，因為{a，b，g，e，c}是格S的子格，而這個子格是與例2中的五角格同構的，所以格S不是模格。

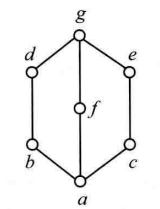圖3