斯坦納—雷米歐斯定理是雷米歐斯、斯坦納等人證明的一個數學定理,故得名。
該定理為:如果三角形中兩內角平分線相等,則此三角形必為等腰三角形。
基本介紹
- 中文名:斯坦納—雷米歐斯定理
- 提出者:1840年
- 套用學科:數學
- 適用領域範圍:平面幾何
發展簡史,驗證推導,證明1,證明2,證明3,證明4,證明5(錯誤,未證BD平分∠E'BC),
發展簡史
這一命題的逆命題:“等腰三角形兩底角的平分線長度相等”,早在二千多年前的《幾何原本》中就已作為定理,證明過程想必大家都會。但上述命題在《幾何原本》中隻字未提。
直到1840年,雷米歐斯(C.L.Lehmus)在他給斯圖姆(C.Sturm)的信中提出請求給出一個純幾何證明。斯圖姆沒有解決,就向許多數學家提出這一問題。首先給出證明的是瑞士幾何學家斯坦納(J.Steiner,1796~1863),因而這一定理就稱為斯坦納—雷米歐斯定理。
繼斯坦納之後,這一定理的豐富多彩的證明陸續發表,但大多是間接證法,直接證法難度頗大。一百多年來,吸引了許多數學家和數學愛好者。
驗證推導
證明1
如圖,設∠ABD=∠DBC=β,∠ACE=就ECB=γ,
則在△EBC與△DBC中:sin(2β+γ)/ sin2β= BC/CE = BC/BD = sin(β+2γ)/ sin2γ(正弦定理)
∴sin(2β)sin(β+2γ) - sin(2γ)sin(2β+γ) =0
∴2sinβcosβsin(β+2γ) - 2sinγcosγsin(2β+γ) =0(二倍角公式)
∴sinβ[sin(2β+2γ)+sin(2γ)] - sinγ[sin(2β+2γ)+ sin(2β)]=0(積化和差)
∴sinβ[sin(2β+2γ)+2sinγcosγ] - sinγ[sin(2β+2γ) + 2sinβcosβ]=0(二倍角公式)
∴sin(2β+2γ)(sinβ-sinγ) + 2sinβsinγ(cosγ- cosβ)=0(重新分組並提取公因式)
∴sin(2β+2γ){cos[(β+γ)/2]sin[(β-γ)/2])} + 2sinβsinγ{sin[(β+γ)/2]sin[(β-γ)/2]}=0
→sin[(β-γ)/2]{sin(2β+2γ)cos[(β+γ)/2] + 2sinβsinγsin[(β+γ)/2]}=0(和差化積)
又顯然上式的後一個因式的值大於零
∴sin[(β-γ)/2]=0
∴β=γ
∴AB=AC. 證畢!
證明2
已知:如圖所示,在△ABC中,∠ABC的平分線交AC於點D,∠ACB的平分線交AB於點E,BD=CE。
求證:AB=AC
證明:
設∠ABD=∠CBD=α,∠ACE=∠BCE=β
如圖所示,分別以BD,CE為底邊,(α+β)為底角,作等腰△EBD和等腰△GEC,使點F和點A在BD的同側,點G和點A在CE的同側,連線AF,AG,CF,BG,則∠FBD=∠FDB=∠GEC=∠GCE=α+β,FB=FD=GE=GC,∠BFD=∠EGC=180°-2α-2β=∠BAC
∴A,D,B,F四點共圓,A,E,C,G四點共圓(四點共圓的判定)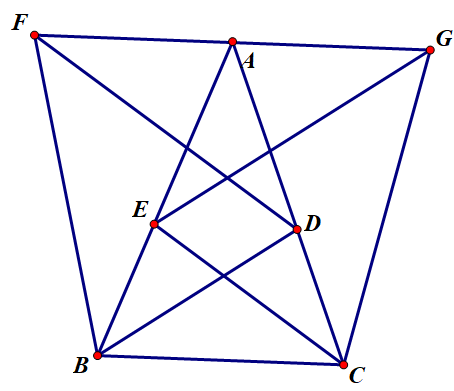 證明2-圖片
證明2-圖片
 證明2-圖片
證明2-圖片∴∠BFA=∠BDC=180°-α-2β,∠FAC=180°-∠FBD=180°-α-β,∠CAG=∠GEC=α+β(四點共圓的性質)
∴∠FAC+∠CAG=180°
∴F,A,G三點共線
∴∠BFG+∠BCG=∠BFA+∠BCE+∠GCE=(180°-α-2β)+β+(α+β)=180°
∴B,C,G,F四點共圓
又∵BF=CG
∴FG//BC
∴2β=∠ACB=∠CAG=α+β
∴α=β
∴∠ABC=∠ACB
∴AB=AC
證明3
如圖,將△AEC繞點O(點O為BE和CD的中垂線的交點)逆時針旋轉,使EC與BD重合,A的對應點為A'。
設BD與CE交於I,則I為△ABC的內心,AI平分∠BAC,則旋轉後AI的對應線為A'I'。連線AA',A'B。
∵∠DA'B=∠BAC(旋轉對應角)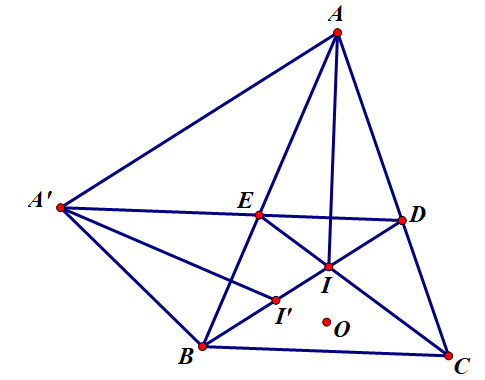

∴A、A'、B、D四點共圓
∴∠AA'D=∠ABD
∵∠AID=∠ABD+∠BAI(外角定理)
∴∠AID=∠AA'D+∠I'A'D=∠AA'I'
∴A、A'、I'、I四點共圓
∵AI=A'I'
∴四邊形AA'I'I是等腰梯形
∴AA'∥II'
即AA'∥BD
∵A、A'、B、D四點共圓
∴四邊形AA'BD是等腰梯形
∴AB=A'D=A'C'
∵A'C'=AC
∴AB=AC
定理證畢
證明4
設CE,BD為△ABC的兩條角平分線。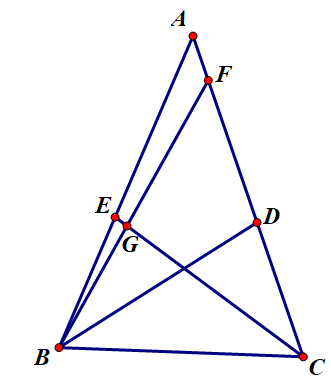 證明4-圖片
證明4-圖片
 證明4-圖片
證明4-圖片假設AC>AB,則∠ABC>∠ACB
∴∠ABD=∠DBC>∠ACE=∠ECB
在∠ABD內部作∠FBD=∠ACE,BF交AC於F,交CE於G,
則∠FBC=∠FBD+∠DBC>∠ACE+∠ECB=∠FCB
∴FB<FC
∵∠FBD=∠ACE,∠BFD=∠GFC
∴△FBD∽△FCI
∴BD/CG=FB/FC<FC/FC=1
∴BD<CG<CE
這與“BD=CE"的已知條件矛盾,所以假設不成立
∴AC≤AB
同理AB≤AC
∴AB=AC
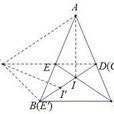
證明5(錯誤,未證BD平分∠E'BC)
設CE,BD為△ABC的兩條角平分線。
過B,C,D作圓,交直線CE於不同於C的一點E'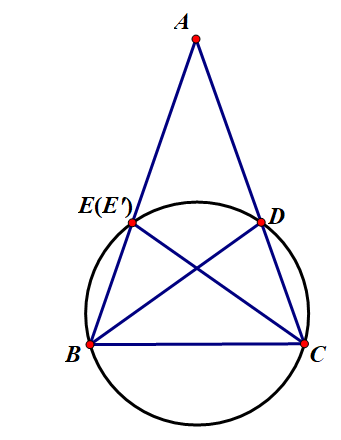 證明5-圖片
證明5-圖片
 證明5-圖片
證明5-圖片∵BD平分∠ABC,CE‘平分∠ACB
∴⌒CD=⌒DE',⌒DE'=⌒E'B
∴⌒BE'D=⌒BE'+⌒E'D=⌒E'D+⌒DC=⌒E'DC
∴CE'=BD=CE
∴E與E'重合
∴B,C,D,E四點共圓
∵CE=BD
∴∠ABC=∠ACB
∴AB=AC