扭率張量

在微分幾何中，撓率或稱撓率此一概念是刻畫沿著曲線移動的標架的扭曲或螺旋的方法。例如曲線的撓率，出現在弗萊納公式中，量化了一條曲線變化時關於它的切矢量的扭曲程度（更確切的說弗萊納標架關於切矢量的旋轉）。在曲面的幾何中，“測地撓率”描述了曲面關於曲面上一條曲線的扭曲。相伴的曲率概念度量了沿著曲線的活動標架“沒有扭曲的轉動”。

基本介紹

• 中文名：扭率張量
• 分類：數理科學

簡介

在裝備一個仿射聯絡（即切叢的一個聯絡）的微分流形上，撓率與曲率構成了聯絡的兩個基本不變數。在這種意義下，撓率給出了切空間關於一條曲線平行移動怎樣扭曲的內蘊刻畫；而曲率描述了切空間沿著曲線怎樣旋轉。撓率可具體的描述為一個張量，或一個矢量值2-形式。如果 ∇ 是微分流形上一個聯絡，那么撓率張量用矢量場X與Y表示定義為：

這裡 [X,Y] 是矢量場的李括弧。

撓率在測地線幾何的研究特別重要。給定一個參數化測地線系統，我們一定指定一族仿射聯絡具有這些測地線，但是具有不同的撓率。具有惟一“吸收撓率”的聯絡，將列維-奇維塔聯絡推廣到其他，也許沒有度量的情形（比如芬斯勒幾何）。吸收撓率在G-結構與嘉當等價方法的研究中也起著重要的作用。撓率通過關聯的射影聯絡在研究測地線非參數族也很有用。在相對論中，這種想法以愛因斯坦-嘉當理論的形式提供了工具。

撓率張量

設M是切叢上帶有聯絡 ∇ 的流形。撓率張量（有時也稱為嘉當（撓率）張量）是一個矢量值 2-形式，定義在矢量場X於Y上

這裡 [X,Y] 是兩個矢量場的李括弧。由萊布尼茲法則，對任何光滑函式f有T(fX,Y) =T(X,fY) =fT(X,Y)。所以T是一個張量，儘管是用非張量的共變導數定義的：它給出了切矢量上的一個 2 形式，但共變導數隻對矢量場有定義。

撓率張量的分量

撓率張量在切叢的局部截面的基(e1, ...,en) 下可寫成分量{\displaystyle T^{c}{}_{ab}}。令X=ei，Y=ej，引入交換子係數 γ

如果基是和樂的，則李括弧變為零， ，從而 。特別地（見下），測地線方程確定聯絡的對稱部分，而撓率張量確定反對稱部分。

撓率形式

撓率形式，是撓率的另一種刻畫，適用於M的標架叢FM。這個主叢裝備有一個聯絡形式ω，一個gl(n)-值的 1-形式將豎直矢量映到gl(n) 中的右作用的生成元，且通過在gl(n) 上的伴隨表示等變糾纏於 GL(n) 在 FM的切叢上的右作用。標架叢也帶有一個典範 1 形式θ，取值於R，定義在標架u∈ FxM（視為一個線性函式u:R→ TxM）為

這裡 π: FM→M是主叢的投影映射。那么撓率形式是

等價地， Θ = Dθ，這裡D是由聯絡確定的外共變導數。

撓率形式是一個取值於R的（水平）扭曲形式，意味著在g∈ Gl(n) 的右作用下等變：

這裡g通過它在R上的基本表示作用在左邊。

曲率形式與比安基恆等式

曲率形式是gl(n)-值 2-形式

這裡，D同樣表示外共變導數。用曲率形式和撓率形式表示，相應的比安基恆等式為：

進一步，我們可以從曲率形式和撓率形式復原曲率和撓率。在 FxM中的點u，我們有

這裡u:R→ TxM是確定纖維中標架的函式，且矢量通過 π的提升與選取無關，因為曲率和撓率形式是水平的（它們在不確定的豎直矢量上為 0）。

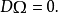
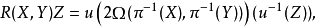
標架中的曲率形式[編輯]參見：聯絡形式

撓率形式可用底流形M上的聯絡形式，在切叢的一個特殊的標架 (e1,...,en) 下寫出。聯絡形式表述這些截面的外共變導數

切叢的焊接形式（關於這個標架）是ei的對偶基θ∈ TM，所以 θ

那么撓率 2-形式有分量

在最右邊的表達式中，

是撓率張量的標架分量，由首先的定義給出。

容易證明 Θ像張量一個變化：如果另一個標架

對某個可逆矩陣值函式 (gi)，那么

換句話說，Θ 是 (1,2) 型張量（一個反變、兩個共變指標）。

做為另一種選擇，焊接形式能用無標架形式刻畫為M上的 TM-值 1形式θ，在對偶同構 End(TM) ≈ TM⊗ TM下對應於切叢的恆等同態。則撓率 2-形式是

的一個截面，由

給出。這裡D是外共變導數（更多細節參見聯絡形式）。

特徵描述與解釋

這一節中總是假設：M是微分流形，∇ 是M切叢上的共變導數除非另外指明。

仿射進化[編輯]

假設xt是M上一條曲線。xt的仿射進化定義為 Tx0M中惟一的曲線Ct使得

這裡

是與 ∇ 關聯的平行移動。

特別地，如果xt是一個閉環路，則Ct是否閉取決於聯絡的撓率。從而撓率解釋為曲線的 development 的螺位錯。這樣，撓率與聯絡的和樂轉移分量聯繫起來。相伴的曲率概念描繪了無窮小線性變換（在黎曼聯絡情形或為旋轉）。

參考標架的扭曲

在經典曲線的微分幾何中，弗萊納公式描述了一個特別的活動標架（弗萊納標架）沿著一條曲線怎樣“扭曲”。用物理語言，撓率對應於一個假想的沿著曲線的陀螺的角動量。

帶有（度量）聯絡的流形可類比地解釋。假設一個觀察者沿著這個聯絡下的測地線移動。這個觀察者通常認為自己是在慣性參考系中，因為她沒有經歷過加速度。另外假設觀察者攜帶著一個剛性直測量桿系統（一個坐標系）。每根桿都是直線段，一條測地線。假設每根桿沿著軌道都是平行移動，這些桿是沿著軌跡物理的“攜帶”的事實意味著是“李拖拽”或傳播，所以沿著切矢量每根桿子的李導數為零。類似於弗萊納標架上的陀螺，它們可能經受力矩（或扭力）。這個力便由撓率衡量。

更準確地，假設觀察者沿著測地線 γ(t) 移動，攜帶著一個測量桿。當觀察者移動時，桿子掃過一個曲面。沿著這個曲面有一個自然坐標系 (t,x)，這裡t是由觀察者確定的時間參數，x是沿著測量桿的長度。測量桿須沿著曲線平行移動的條件為

從而，撓率由

給出。如果不是零，則桿上標出的這點（點x= 常曲線）的軌跡為螺旋而不是測地線。它們將繞著觀察者旋轉。

這種撓率的解釋在平行引力理論中扮演著重要的角色。平行引力理論，也稱為愛因斯坦-嘉當理論，是相對論的一種替代性表述。

纖維的撓率

在材料科學中，特別是彈性理論，撓率的想法也扮演著重要的角色。其中一個問題是藤生長的建模，專注於藤如何能繞著對象纏繞。藤自身模型化為一對相互纏繞的彈性纖維。在其能量極小狀態，藤自然生長成一個螺旋狀。但是藤也有可能伸長以達到廣度（或長度）最大化。在此情形，藤的撓率與這對纖維的撓率有關（或等價地，連結兩條纖維的帶子的曲面撓率），這反映了藤的長度最大化（測地線）布局與能量最小化布局之間的差異。

撓率與渦旋

在流體力學中，撓率自然與渦線相關。

測地線與撓率的吸收

假設 γ(t) 是M上一條曲線。則 γ 是一條仿射參數化測地線如果

對屬於 γ的定義域中所有時間t（這裡點表示關於t求導，得到了 γ(t) 處切矢量 ）。每條測地線由初始t=0 切矢量 惟一確定。

聯絡的撓率的一個運用涉及到聯絡的測地波浪（geodesic spray）：粗略地講為所有仿射參數化測地線。

用測地波浪將聯絡分類時，不同撓率不能區分開來：

• 兩個聯絡 ∇ 與 ∇′ 具有相同的仿射參數化測地線（即相同的測地波浪），只在撓率有區別。
  

更準確地，如果X與Y是p∈M的一對切矢量，那么令

是兩個聯絡的差，用X與Y從p處的任意擴張計算。由萊布尼茲乘積法則，我們看出 Δ 事實上與X和Y如何擴張無關（所以定義了M上一個張量）。設S與A分別為 Δ 的對稱與交替部分：

則是撓率張量之差。

∇ 與 ∇′ 定義了相同的仿射參數化測地線族若且唯若S(X,Y) = 0。

換句話說，兩個聯絡之差的對稱部分決定了它們是否具有相同的參數化測地線，然而差的斜對稱部分由這兩個聯絡的相對撓率決定。另一個推論是

• 給定任何仿射聯絡 ∇，存在惟一一個無撓聯絡 ∇′ 具有共同的仿射參數化測地線。
  

這是黎曼幾何基本定理到（也許無度量）仿射聯絡的一個推廣。選出從屬於一族參數化測地線惟一的聯絡也稱為撓率的吸收，這是嘉當等價方法的一個使用之處。