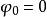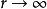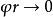托馬斯-費米方程是計算原子中的電荷分布及電場的方程,是托馬斯-費米方法的基本方程,托馬斯-費米方法是在1927年提出的,由提出者E.Fermi(費米)和L.Thomas(托馬斯)而得名。
基本介紹
- 中文名:托馬斯-費米方程
- 外文名:Thomas-Fermi equation
- 學科:量子力學
- 貢獻者:費米和L托馬斯
- 得出於:托馬斯-費米方法
- 用途:計算原於中的電荷分布及電場
- 適用範圍:不適於遠離及靠近原子核處
概念,解析,
概念

(每一“相格”中只能裝進自旋相反的兩個電子).在基態原子中,每一個dV體積元內的電子必須填滿(相空間內的)動量值從零直到某一極大值 為止的相格.此時,電子動能在每一點都取儘可能小的數值.如果把dV體積元內的電子數寫成ndV(n為電子數密度),那么,各點處電子動量的極大值
為止的相格.此時,電子動能在每一點都取儘可能小的數值.如果把dV體積元內的電子數寫成ndV(n為電子數密度),那么,各點處電子動量的極大值 與n的關係為
與n的關係為



在電子數密度為n的地方,一個電子的最大動能值因而等於

其次,設 為靜電勢,假定它在無窮遠處等於零.電子的總能量為
為靜電勢,假定它在無窮遠處等於零.電子的總能量為 .顯然,每個電子的總能量一定等於負值,否則它會運動到無窮遠處去.我們用
.顯然,每個電子的總能量一定等於負值,否則它會運動到無窮遠處去.我們用 代表每點處電子總能量的極大值,
代表每點處電子總能量的極大值, 是一個正的常數;如果
是一個正的常數;如果 不是常數的話,電子就會從
不是常數的話,電子就會從 較小之處運動到
較小之處運動到 較大之處.因此我們可寫出
較大之處.因此我們可寫出








把(1)和(2)式等同起來,即得

這就是原子內各點的電子數密度與勢能的關係式.



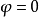




並引進下列新的未知函式 代替
代替 :
:


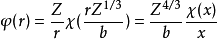
我們得到方程式

其邊界條件為x=0時 以及
以及 時疋
時疋 .這個方程不再含有任何參量,因而定義出一個普適的
.這個方程不再含有任何參量,因而定義出一個普適的 函式.下表給出了(7)式數值積分後所得的
函式.下表給出了(7)式數值積分後所得的 函式值.
函式值.





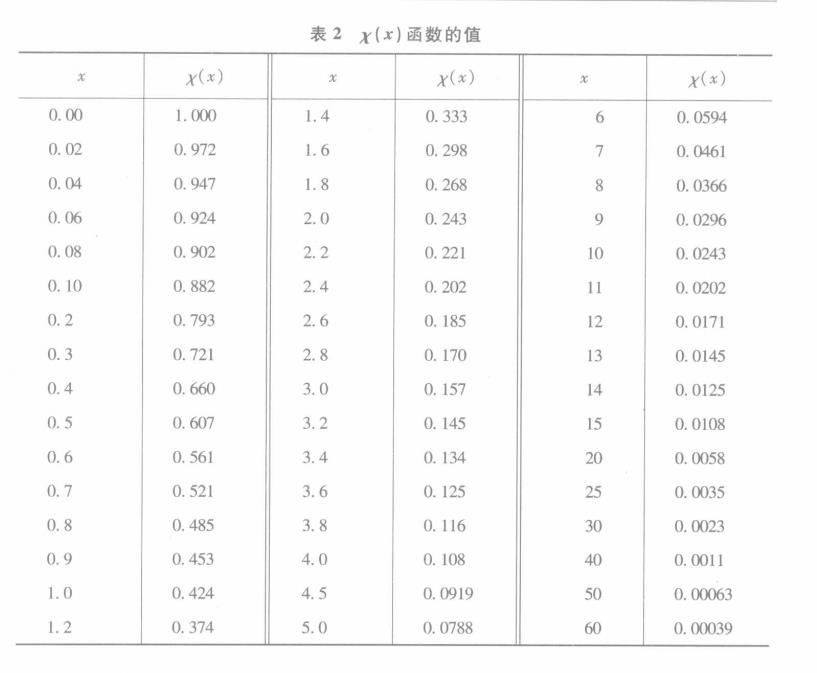 函式的值
函式的值
導數 在r=0處的值等於
在r=0處的值等於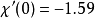 .因此當
.因此當 時
時 函式具有
函式具有 的形式,相應的勢
的形式,相應的勢 為:
為:

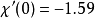





第一項是核場的勢,第二項是電子在原點的勢(通常的單位制中為 ),把(6)代入(3)中,可得電子數密度的下列表式:
),把(6)代入(3)中,可得電子數密度的下列表式:


解析
我們看到,按托馬斯一費米模型,不同原子中的電荷密度分布是相似的,並以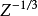 為特徵長度(在通常的單位制中為
為特徵長度(在通常的單位制中為 即玻爾半徑除以
即玻爾半徑除以 ).如果以原子單位量度距離,那么,電子數密度達到最大值的那個距離對所有的z都是一樣的。因此可以這樣說,原子序為Z的原子中大多數的電子與原子核的距離約為
).如果以原子單位量度距離,那么,電子數密度達到最大值的那個距離對所有的z都是一樣的。因此可以這樣說,原子序為Z的原子中大多數的電子與原子核的距離約為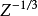 的數量級。數值計算表明,原子中電子總電荷的一半處於半徑為
的數量級。數值計算表明,原子中電子總電荷的一半處於半徑為 的球內。
的球內。
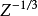


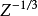

同樣的考慮表明,原子中電子的平均速度(與能量的平方根同一數量級)約為 的數量級.
的數量級.

托馬斯一費米方程在遠離原子核以及靠近原子核處都不能適用.它在近距離處的適用範圍,由不等式 (遠大於第一玻爾“半徑”的距離)所限制;距離更小時,準經典近似在核庫侖場內不再成立.令式
(遠大於第一玻爾“半徑”的距離)所限制;距離更小時,準經典近似在核庫侖場內不再成立.令式 中的
中的 ,我們求得距離r的下限為1/Z.在複雜原子中,當r很大時準經典近似也不能成立.容易證明,當
,我們求得距離r的下限為1/Z.在複雜原子中,當r很大時準經典近似也不能成立.容易證明,當 時,電子的德布羅意波長與距離本身成為同一數量級,準經典條件無疑遭到破壞.這一點,由估計(2),(4)式各項之值可以確信;實際上,由於(4)式不含Z,這個結論無需計算就能明顯看出來.
時,電子的德布羅意波長與距離本身成為同一數量級,準經典條件無疑遭到破壞.這一點,由估計(2),(4)式各項之值可以確信;實際上,由於(4)式不含Z,這個結論無需計算就能明顯看出來.




由此可見,托馬斯一費米方程的適用範圍,局限在大於1/Z和小於1的距離內.事實上在複雜原子中,絕大多數的電子實際上都是處於這個適用範圍內.
後一種情況表明,托馬斯一費米模型中原子的“外邊界”位於 處,也就是原子的線度並不依賴於Z.與此相應,外電子的能量亦即原子的電離勢也與Z無關.
處,也就是原子的線度並不依賴於Z.與此相應,外電子的能量亦即原子的電離勢也與Z無關.

藉助於托馬斯一費米方法,可以算出總的電離能E,即移掉中性原子內全部電子所必需的能量.為此目的,我們有必要算出具有托馬斯一費米分布的原子內電荷的靜電能;我們所求的總能量等於這個靜電能的一半,因為在按庫侖定律作用的多粒子系統中,它的平均動能等於平均勢能的-1/2(根據位力定理).E和Z的依賴關係可以根據以下的簡單考慮事先確定:在電荷為z的核場內運動的Z個電子,在與核的平均距離為 處的靜電能,與
處的靜電能,與 成正比.數值計算的結果為
成正比.數值計算的結果為 .這個對Z的依賴關係與實驗數據很符合;可是係數的經驗值接近於16.
.這個對Z的依賴關係與實驗數據很符合;可是係數的經驗值接近於16.



我們已經提到過,常數 取不等於零的正值時對應於電離原子。如果我們通過
取不等於零的正值時對應於電離原子。如果我們通過 來定義
來定義 函式,所得的
函式,所得的 方程就和原先的(7)式相同。但是,我們現在感興趣的不是在無窮遠處等於零的中性原子那樣的解,而是在有限值
方程就和原先的(7)式相同。但是,我們現在感興趣的不是在無窮遠處等於零的中性原子那樣的解,而是在有限值 處等於零的解;這樣的解,對任意一個
處等於零的解;這樣的解,對任意一個 值講來,都是存在的.在
值講來,都是存在的.在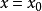 點處,電荷密度和
點處,電荷密度和 一起等於零,但是勢能仍保持有限值.
一起等於零,但是勢能仍保持有限值. 值可按以下方式與電離度相聯繫。按照高斯定理,半徑為r的球內的總電荷等於
值可按以下方式與電離度相聯繫。按照高斯定理,半徑為r的球內的總電荷等於 ,把
,把 代入上式,即得離子的總電荷z;由於
代入上式,即得離子的總電荷z;由於 ,故
,故






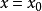






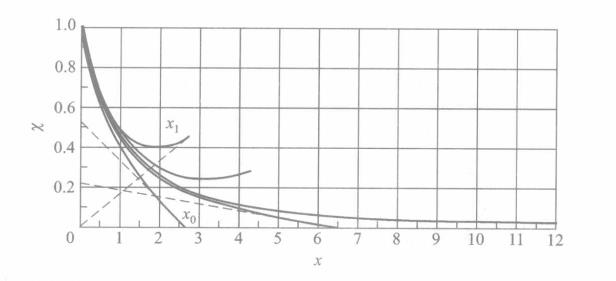 函式曲線
函式曲線
在 的球內總電荷等於零(在圖上,這一點顯然就是切線通過原點的那個點)。如果在
的球內總電荷等於零(在圖上,這一點顯然就是切線通過原點的那個點)。如果在 點處把曲線截斷,我們就定義了一個界面電荷密度不等於零的中性原子的
點處把曲線截斷,我們就定義了一個界面電荷密度不等於零的中性原子的 .在物理上,這相當於束縛在某一給定有限體積內的“壓縮”原子。
.在物理上,這相當於束縛在某一給定有限體積內的“壓縮”原子。



托馬斯一費米方程沒有計及電子間的交換作用。這種作用的效應要比 小一個數量級。因此,在托馬斯一費米方法中計及交換作用時,還需同時計及同一數量級的其它各種效應。
小一個數量級。因此,在托馬斯一費米方法中計及交換作用時,還需同時計及同一數量級的其它各種效應。