弦勾求股作圖亦稱弦股求勾作圖，是基本作圖題(作圖成法)之一。我國古代，把直角三角形的兩條直角邊叫做勾和股，斜邊叫做弦。弦勾求股作圖即已知直角三角形的一直角邊和一斜邊求做另一直角邊。
基本介紹
- 中文名：弦勾求股作圖
- 別稱：弦股求勾作圖
- 所屬學科：數學
- 所屬問題：平面幾何（三角形）
基本介紹,相關歷史介紹,
基本介紹
弦勾求股作圖亦稱弦股求勾作圖，即作
，是基本作圖題(作圖成法)之一。具體表述為：已知線段a和b，且a>b，求作線段x，使 ，其具體作法是：
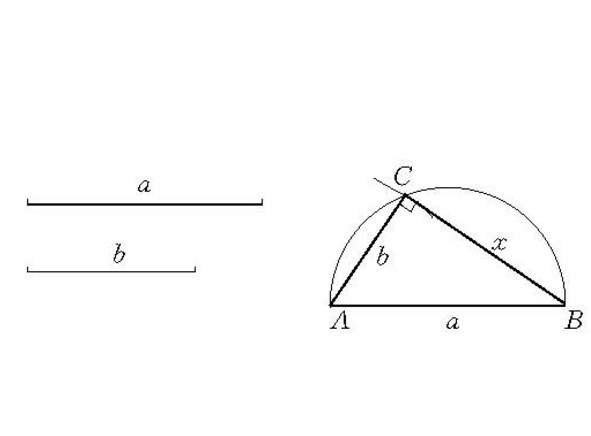
1.作線段AB=a；
2.以AB的中點為圓心，AB/2為半徑作半圓弧；
3.以A為圓心，線段b為半徑作弧，交半圓弧於點C；
4.連結BC，則線段BC為所求線段x。
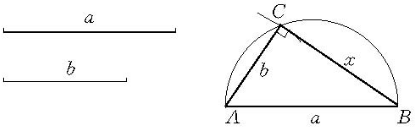圖1相關歷史介紹
《周髀算經》
我國古代，把直角三角形的兩條直角邊叫做勾和股，斜邊叫做弦。在數學古書《周髀算經》中，曾記載了周公和商高的一段問答，其中談到“故折矩，以為勾廣三，股修四，徑隅五”。“勾廣”就是勾長，“股修”就是股長，“徑隅”就是弦長。這句話的意思是說，如果將一根直尺折成一個直角，若短直角邊的長為3，長直角邊的長為4，那么斜邊的長一定為5。在《周髀算經》中記載的榮方和陳子的問答中，談到了由勾股求弦的一般方法“勾股各自乘，並而開方除之”。可見古代勞動人民已將勾股定理運用於生產實踐之中。一般認為《周髀算經》成書於公元前1世紀，可見我國至少在2100年前就發現了勾股定理。
解勾股形
《九章》勾股章提出了若干已知勾股形三邊中二者的和差等因素，求其邊長的例題。趙爽、劉徽、賈憲先後作了進一步的發展，提出了一般性的公式及其證明。
國內外流行的印度蓮花問題實際上是《九章》“引葭赴岸”題的改寫。此題是：有一水池，方1丈，一株葭[jia佳，初生的蘆葦]生在中央，高出水面1尺，引葭赴岸，恰恰與岸邊相齊。問水深、葭長各多少?如圖2，劉徽指出，水池邊長的一半為勾a，水深為股b，葭長為弦c，葭高於
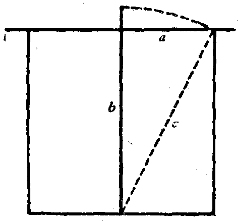圖2 引葭赴岸
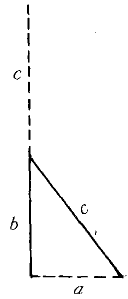圖3 竹高折地水面者是弦股差c-b，這是已知勾與弦股差，求股、弦的問題：
1989年語文高考試卷有一古文今譯題便采自《九章》勾股章“竹高折地”問：今有一株竹高1丈，被折斷，末梢抵地，抵地處距竹根3尺，問剩餘高多少?如圖3，劉徽指出，抵地處至竹根距離是勾a，剩餘的高是股b，折斷部分是弦c，則竹高就是股弦和c+b，此是已知勾與股弦和，求股的問題：
這兩類題目互相返覆，劉徽以出入相補原理證明之。
有一門戶，高比寬多6尺8寸，兩角相距1丈。問此門戶高、寬各多少?劉徽認為，將戶寬作為勾a，高為股b，兩角相距為弦c，那么這是一個已知弦c與股勾差b-a，求勾、股的問題。《九章》的解法經劉徽改寫成
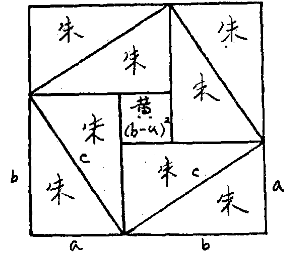圖4 已知弦與股勾差求勾股的證明有一門戶不知高、寬，有人持一竹竿，不知長短，橫著出門，長了4尺，豎著出門，長了2尺，斜著恰好能出門。問門的高、寬、斜各多少?劉徽把門戶的高、寬、斜分別作為勾、股、弦，此題是已知弦勾差c-a、弦股差c-b，求勾、股、弦的問題。《九章》給出的公式是：
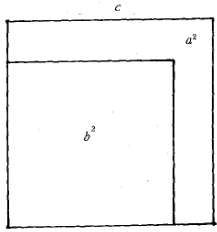圖5（1）已知弦勾差弦股差求勾股弦的證明
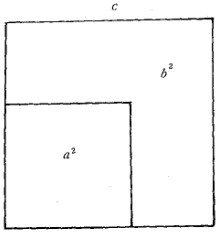圖5（2）已知弦勾差弦股差求勾股弦的證明
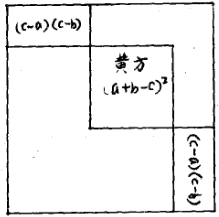圖5（3）已知弦勾差弦股差求勾股弦的證明為了證明這些公式，劉徽首先指出了在弦冪中勾冪與股冪的相互位置，或矩於表，或方於里：若股冪為方形，則勾冪作為勾矩居於股方之表，如圖5(1);反之亦然，如圖5(2)。劉徽將其中一個圖形旋轉180°，與另一個重合，則成為圖5(3)的情形。勾矩c2-b2與股矩c2-a2的面積之和應為弦冪c2。在圖中，這兩者在兩角重合於兩個以c-b為寬、c-a為長的長方形，其面積為2(c-a)(c-b)。而弦冪中卻有一個以a+b-c為邊長的小黃方未被勾矩與股矩填滿。顯然，小黃方的面積(a+b-c)2應等於2(c-a)(c-b)，開方
b=(a+b-c)+(c-a)，
c=(a+b-c)+(c-b)+(c-a)便證明了上述三式。
北宋賈憲把《九章》解勾股形的四個類型的方法抽象成一般性公式。楊輝又進而總結出a、b、c、c±a、c±b、b±a、a+b±c、c±(b-a)13種關係及變成b-a、c-b、a+b-c的段數，稱作“勾股生變十三名圖”。這13種關係包括了勾股形中勾、股、弦及其和、差的全部可能的關係，對勾股理論起著提綱挈領的作用。
