康托爾公理指的是在Zermelo-Fränkel集合論中,聲稱任何集合A的冪集(所有子集的集合)的勢嚴格大於A的勢。康托爾定理對於有限集合是明顯的,但是令人驚奇的是它對於無限集合也成立。特別是,可數無限集合的冪集是不可數無限的。要展示康托爾定理的對於無限集合的有效性,只需要測試一下下面證明中無限集合。
基本介紹
- 中文名:康托爾公理
- 外文名:Cantor's theorem
- 學科:數學
證明





在X是可數無限時對證明的詳細解釋


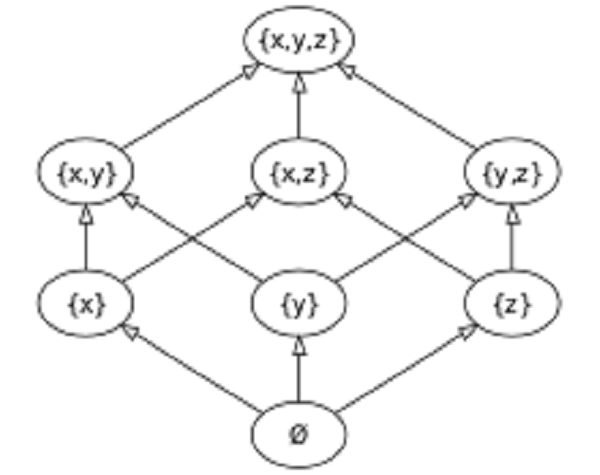
康托爾公理指的是在Zermelo-Fränkel集合論中,聲稱任何集合A的冪集(所有子集的集合)的勢嚴格大於A的勢。康托爾定理對於有限集合是明顯的,但是令人驚奇的是它對於無限集合也成立。特別是,可數無限集合的冪集是不可數無限的。要展示康托爾定理的對於無限集合的有效性,只需要測試一下下面證明中無限集合。







康托爾公理指的是在Zermelo-Fränkel集合論中,聲稱任何集合A的冪集(所有子集的集合)的勢嚴格大於A的勢。康托爾定理對於有限集合是明顯的,但是令人驚奇的是它...
數學形式主義的一個早期成功的例子為希爾伯特對歐幾里得幾何的公式化,以及相關地,對此些公理相容性的確定。在更廣的方面來看,還有人企圖將所有數學放在康托爾的集合...
四、康托爾閉區間套模型(可歸入第三個模型)實數公理實數的基本定理 編輯 實數系的基本定理也稱實數系的完備性定理、實數系的連續性定理,這些定理分別是確界存在...
康托爾-伯恩施坦定理也叫作定理康托爾-伯恩斯坦-施洛德定理(Cantor-Bernstein-Schroeder theorem),是集合論中的一個基本定理,得名於康托爾、伯恩斯坦和 Ernst ...
格奧爾格·康托爾(Cantor,Georg Ferdinand Ludwig Philipp,1845.3.3-1918.1.6)德國數學家,集合論的創始人。生於俄國聖彼得堡。父親是猶太血統的丹麥商人,母親出身...
此外,“一些現在看來類似...策梅洛的並集和分離公理(Axiom of Separation)的命題”也出現在1899年康托爾給戴德金的信中;不過,就算是這樣,“也沒有證據表明康托...
加以刻畫的,然而公理的背景都是很深刻和直觀的,它們來源於康托爾(G.F.P.Cantor)的集合論,是從經典集合論中整理和抽象出來的基本原則.每一公理都刻畫集合的某...
1874年格奧爾格·康托爾猜測在可列集基數和實數基數之間沒有別的基數,這就是著名的連續統假設。它又被稱為希爾伯特第一問題,在1900年第二屆國際數學家大會上,...
完整的公理體系,它由五組公理組成,即關聯公理、順序公理、契約公理、連續公理和...直線完備公理等價於康托爾公理。直線完備公理保證了直線上的一切點可以和實數一一...
基於自然數的兩種功能層次,即表達個數的概念和表達順序的概念,19世紀末出現了著名的康托爾基數公理和皮亞諾序數公理,從數學邏輯的角度對什麼是個數和什麼是順序號...
冪集康托猜想 編輯 不存在一個集合, 它的勢嚴格大於可數集的勢, 同時嚴格小於...也不能被證偽--就是說不能從現有的數學公理體系推演出該結論或者否定該結論。...
