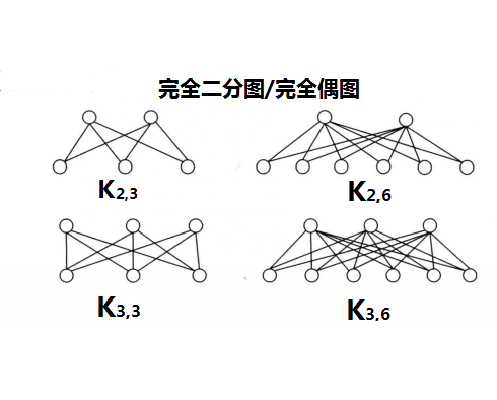
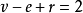設G=(V,E)為二分圖,V=XUY,且X中的任一頂點與Y中每一個頂點均有且僅有唯一的一條邊相連,則稱G為完全二分圖或完全偶圖。
基本介紹
- 中文名:完全二分圖
- 外文名:complete bipartite graph
- 所屬領域:數學
- 別名:完全偶圖
基本概念,相關概念,相關結論,定理1,推論1,定理2,推論2,推論3,推論4,推論5,
基本概念
直觀地講,對於平面上的n個點,把其中的一些點對用曲線或直線連線起來,不考慮點的位置與連線曲直長短,這樣形成的一個關係結構就是一個圖。記成G=(V,E),V是以上述點為元素的頂點集,E是以上述連線為元素的邊集。
如果圖的兩頂點間有邊相連.則稱此兩頂點相鄰,每一對頂點都相鄰的圖稱為完全圖,否則稱為非完全圖.設 為n階無向簡單圖,若
為n階無向簡單圖,若 中每個頂點均與其餘的
中每個頂點均與其餘的 個頂點相鄰,則稱
個頂點相鄰,則稱 為n階無向完全圖,簡稱n階完全圖,記做
為n階無向完全圖,簡稱n階完全圖,記做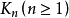 。設
。設 為n階有向簡單圖,若
為n階有向簡單圖,若 中每個頂點都鄰接到其餘的
中每個頂點都鄰接到其餘的 個頂點,又鄰接於其餘的
個頂點,又鄰接於其餘的 個頂點,則稱
個頂點,則稱 是n階有向完全圖。
是n階有向完全圖。




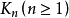





圖1分別列出了 。圖2分別列出了1階有向完全圖、2階有向完全圖、3階有向完全圖。
。圖2分別列出了1階有向完全圖、2階有向完全圖、3階有向完全圖。

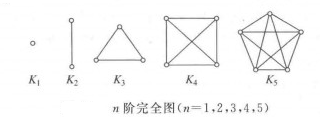 圖1
圖1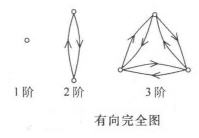 圖2
圖2若 (這裡
(這裡 表示頂點集
表示頂點集 中元素的個數),且
中元素的個數),且 中無相鄰的頂點對,
中無相鄰的頂點對, 中亦然,則稱圖
中亦然,則稱圖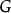 為二分圖;特別地,若對任意
為二分圖;特別地,若對任意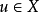 ,
, 與
與 中每個頂點相鄰,則稱圖G為完全二分圖(complete bipartite graph),或稱完全偶圖,記為
中每個頂點相鄰,則稱圖G為完全二分圖(complete bipartite graph),或稱完全偶圖,記為 。
。






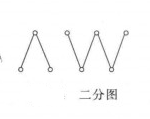 圖3
圖3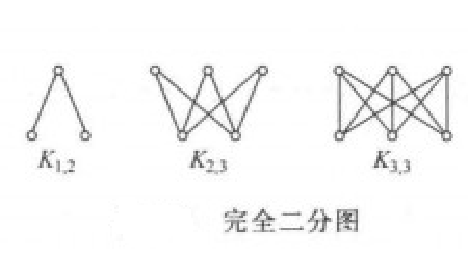 圖4
圖4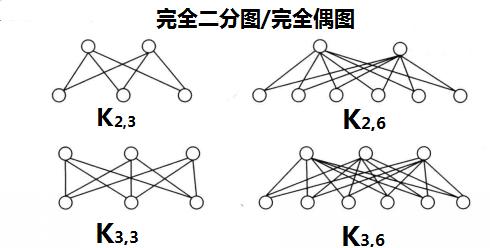 圖5
圖5相關概念
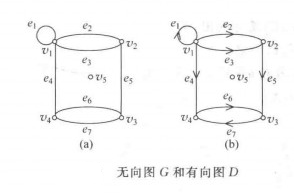 圖6
圖6任兩頂點間最多有一條邊,且每條邊的兩個端點皆不重合的圖,稱為簡單圖。
設 是邊
是邊 的端點,則稱v與e相關聯,與頂點v關聯的邊數稱為該頂點的度,記為
的端點,則稱v與e相關聯,與頂點v關聯的邊數稱為該頂點的度,記為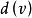 ,度為奇數的頂點稱為奇頂點,度為偶數的頂點稱為偶頂點。可以證明
,度為奇數的頂點稱為奇頂點,度為偶數的頂點稱為偶頂點。可以證明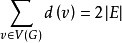 ,即所有頂點的度數之和是邊數的2倍,且由此可知奇頂點的總數是偶數。
,即所有頂點的度數之和是邊數的2倍,且由此可知奇頂點的總數是偶數。


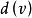
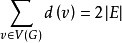
設 ,其中
,其中 與
與 和
和 關聯,稱
關聯,稱 是圖
是圖 的一條道路,k為路長,
的一條道路,k為路長, 為起點,
為起點, 為終點;各邊相異的道路稱為跡;各頂點相異的道路稱為軌道。若
為終點;各邊相異的道路稱為跡;各頂點相異的道路稱為軌道。若 是一軌道,則可記為
是一軌道,則可記為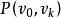 ;起點與終點重合的道路稱為迴路;起點與終點重合的軌道稱為圈,即對軌道
;起點與終點重合的道路稱為迴路;起點與終點重合的軌道稱為圈,即對軌道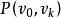 ,當
,當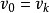 時成為一圈;圖中任兩頂點之間都存在道路的圖,稱為連通圖。圖中含有所有頂點的軌道稱為Hamilton軌,閉合的Hamilton軌道稱為Hamilton圈;含有Hamilton圈的圖稱為Hamilton圖。稱兩頂點
時成為一圈;圖中任兩頂點之間都存在道路的圖,稱為連通圖。圖中含有所有頂點的軌道稱為Hamilton軌,閉合的Hamilton軌道稱為Hamilton圈;含有Hamilton圈的圖稱為Hamilton圖。稱兩頂點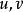 分別為起點和終點的最短軌道之長為頂點
分別為起點和終點的最短軌道之長為頂點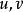 的距離;在完全二分圖
的距離;在完全二分圖 中,
中,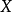 中兩頂點之間的距離為偶數,
中兩頂點之間的距離為偶數,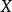 中的頂點與
中的頂點與 中的頂點的距離為奇數。
中的頂點的距離為奇數。





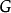


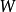
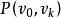
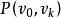
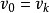
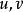
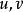

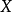
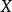

賦權圖是指每條邊都有一個(或多個)實數對應的圖,這個(些)實數稱為這條邊的權(每條邊可以具有多個權)。賦權圖在實際問題中非常有用。根據不同的實際情況,權數的含義可以各不相同。例如,可用權數代表兩地之間的實際距離或行車時間,也可用權數代表某工序所需的加工時間等。
相關結論
定理1
對於圖 ,有
,有 ,其中
,其中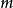 為
為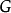 的邊數。
的邊數。


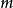
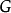
對於圖中的每條邊均關聯2個頂點,在計算度數時,每條邊均提供2度,圖有m條邊,度數共2m。
在有向圖中還有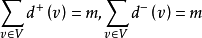 。
。
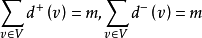
這個定理稱為握手定理,是數學家歐拉於1736年提出,它是圖論中的基本定理,由它還可以得到下面的重要推論。
推論1
任一圖中,奇數度數頂點的個數為偶數。
證明:設 和
和 分別為圖
分別為圖 中度數分別為奇數和偶數的頂點集,且
中度數分別為奇數和偶數的頂點集,且 ,
,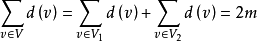 ,則
,則 ,由於
,由於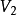 中度數均為偶數,故
中度數均為偶數,故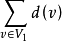 為偶數,只有偶數個奇數的和為偶數,故
為偶數,只有偶數個奇數的和為偶數,故 的個數為偶數。
的個數為偶數。




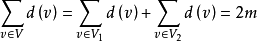

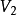
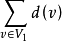

利用推論1可以很方便地判斷給定的度數序列能否構成圖。如度數序列(3,3,3,1)可以畫出圖來,而度數序列(3,3,3,2)不可能畫出圖來。
定理2
推論2
設 是帶
是帶 條邊和
條邊和 個頂點的連通簡單平面圖,其中
個頂點的連通簡單平面圖,其中 ,則
,則 。
。





證明: 由於 是簡單圖,因此
是簡單圖,因此 的每個面的度數至少為3。所以圖
的每個面的度數至少為3。所以圖 的面的度數之和
的面的度數之和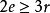 ,其中r為
,其中r為 的面數,由歐拉公式得
的面數,由歐拉公式得 。證畢。
。證畢。



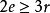


推論3
證明:  的每個面的度數至少為4。證畢。
的每個面的度數至少為4。證畢。

例1 完全圖 和完全二分圖
和完全二分圖 均是非平面圖。
均是非平面圖。


解: 圖 有5個頂點10條邊,而3×5-6=9.即10>9,故由推論2知
有5個頂點10條邊,而3×5-6=9.即10>9,故由推論2知 是非平面圖;圖
是非平面圖;圖 沒有長度為3的圈,且有6個頂點9條邊,因而9>2×6-4。故由推論3知
沒有長度為3的圈,且有6個頂點9條邊,因而9>2×6-4。故由推論3知 是非平面圖。
是非平面圖。




推論4
設 是帶
是帶 條邊,
條邊, 個頂點和
個頂點和 個面的平面圖,則
個面的平面圖,則 ,其中
,其中 為連通分支數。
為連通分支數。






推論5
設 是任意平面圖, 則
是任意平面圖, 則 。
。