基本介紹
- 中文名:完全圖
- 外文名:complete graph
- 領域:數學
- 概念:每對頂點之間都恰連有一條邊的圖
- 分類:有向完全圖,無向完全圖
- 相關名詞:無向圖
簡介
屬性
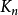
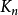
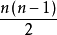
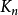
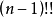
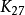
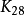
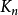
幾何和拓撲
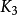
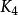
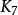
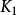
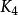
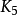
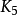
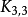
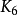
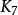
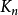
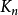
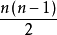
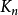
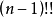
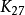
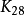
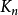
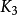
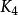
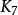
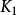
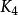
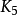
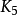
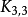
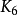
在圖論的數學領域,完全圖是一個簡單的無向圖,其中每對不同的頂點之間都恰連有一條邊相連。完整的有向圖又是一個有向圖,其中每對不同的頂點通過一對唯一的...
無向完全圖是用n表示圖中頂點數目的一種圖,一張圖中每條邊都是無方向的。...... 無向完全圖是用n表示圖中頂點數目的一種圖,一張圖中每條邊都是無方向的。...
《完全圖解系列6本》是2008年9月1日出版的圖書,作者是董志道。本書主要介紹了歷史上不同時期出現的各種宇宙觀,闡述了以宇宙膨脹為基礎的大爆炸理論,為讀者勾畫...
《完全圖像單詞記憶法》全書分7大章節,31個小節。本書摒棄了傳統的按單詞字母順序進行排序的方法,而是將單詞按生活場景進行細分。為了增加閱讀的趣味性,每箇中心單詞...
《完全圖解心理學系列》是一本正文語種為簡體中文的書籍。...... 《完全圖解心理學系列(套裝共4冊)(心理學入門;心理諮詢;身邊心理學;心理療法)》:《心理學入門》...
《完全圖解哲學》是2008年南海出版公司出版的書籍,作者是宋威。...... 《完全圖解哲學》以活潑的文字、有趣的故事和簡明易懂的圖解,呈現東西方哲學在歷史長河中萌發...
《時尚家居完全圖典》是2003年上海辭書出版社出版的圖書,作者是李偉國。...... 《時尚家居完全圖典》是2003年上海辭書出版社出版的圖書,作者是李偉國。...
《完全圖解戀愛心理學》是2008年5月南海出版公司出版的圖書,作者是穆銘。本書主要從心理學的角度詮釋了戀愛心理、成就愛情、愛情的進展等內容。...
《完全圖解三十六計》是2008-年南海出版公司出版的圖書,作者是林斌。...... 《完全圖解三十六計》是2008-年南海出版...除了精彩的文字,我們還使用一頁文字一頁圖...
《完全圖解10分鐘終結各種疼痛》是2010年9月江西科學技術出版社出版的圖書,作者是姜錫萬。該書介紹了治療疼痛的100種伸展療法。...
完全圖解不可思議的人體編輯 鎖定 為什麼心臟不會患癌症?暈車的原理又是什麼呢?許多人對與我們朝夕相伴的身體不夠了解,使我們的身體無法達到物盡其用,更不可能...
《新手上路完全圖解》是2013年機械工業出版社出版的圖書,作者是王志勇。...... 《新手上路完全圖解》是2013年機械工業出版社出版的圖書,作者是王志勇。...
《完全圖形推理(1)》是2005-1-1少年兒童出版社出版的圖書,作者是張鴻雁 / 李曉明。...... 《完全圖形推理(1)》是2005-1-1少年兒童出版社出版的圖書,作者是張...
《完全圖解不可不知的天災地變》是2008-8-1南海出版公司出版的圖書,作者吳悅...... 《完全圖解不可不知的天災地變》是2008-8-1南海出版公司出版的圖書,作者吳...
《完全圖解時間簡史:人人可以讀懂的霍金》作者是(英)霍金,連載網站是搜狐讀書,屬於小說。...
《完全圖解大眾心理學》選擇以圖釋文,以圖代問的形式,通過精美手繪圖詮釋心理學概念,讓讀者在輕鬆愉悅的過程中,了解和掌握心理學變化的特徵和規律,為背負壓力的...
《空調器電控系統維修完全圖》是一本正文語種為簡體中文的書籍。...... 《空調器電控系統維修完全圖》是一本正文語種為簡體中文的書籍。中文名 空調器電控系統維修...
《完全圖解時間簡史》是2008年4月1日南海出版公司出版的圖書,作者是霍金。...... 《完全圖解時間簡史》以《時間簡史》為底本,對霍金的思想進行了系統,全面的解讀...
武器裝備完全圖冊編輯 鎖定 世界上絕大多數的人都熱愛和平,反對戰爭,但是,戰爭中所使用的先進武器裝備畢竟是人類高科技的結晶。因此就引起廣大讀者的關注。當今世界,...
《完全圖解貓的心理》內容匯集了動物行為專家的最新研究成果。創新地採用了“左文右圖”的編輯模式,用百多幅有趣的手繪蠟筆插畫為你完整分析愛貓的心理,帶給你快樂...
《完全圖解諸子百家》在介紹儒、墨、道、法、兵各家的同時,結合最新出土文物,以現代圖解方式詮釋其中的奧妙,將各家的思想特點形象地呈現在讀者眼前,使讀者有機會...
《完全圖解總量經濟學》是2008-07-01南海出版公司出版的圖書,作者是王國強 ...... 《完全圖解總量經濟學》政府和市場的關係為主線,系統介紹了總量經濟學中的凱恩斯...
稀疏圖,數據結構中的一種定義圖。與之相反的是稠密圖。稀疏圖的邊數遠遠少於完全圖,反之,稠密圖的邊數接近於或等於完全圖。...
