基本介紹
- 中文名:多元多項式
- 外文名:multivariate polynomial
- 所屬學科:數學
- 相關概念:字典排序法、一元多項式等
基本知識
相關知識










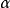
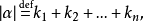


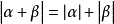

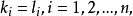

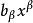

n元多項式的定義


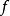
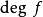

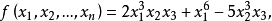
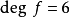

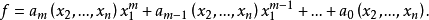
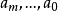
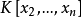
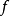
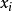
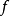
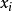



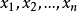
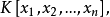
多項式的排序問題

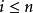



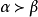
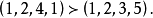
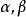
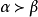

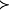
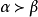
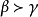

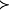

相關性質
定理1
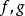
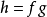
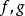



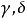

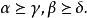
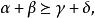

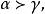


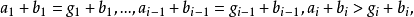

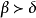

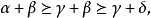



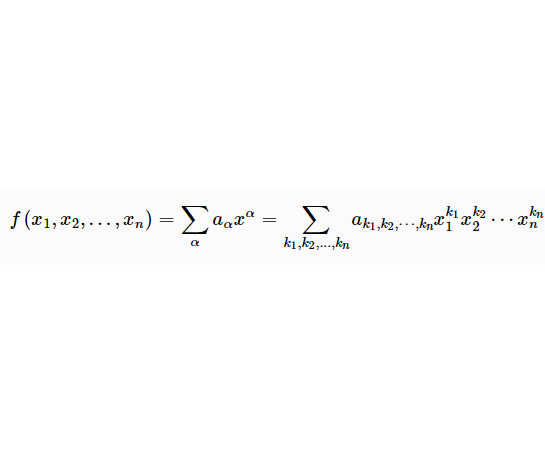










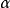
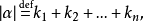


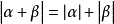

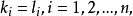

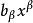



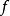
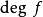

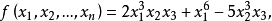
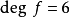

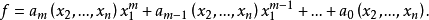
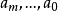
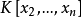
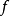
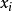
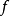
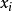



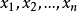
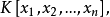

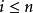



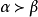
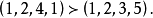
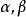
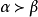

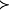
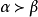
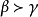

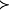

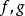
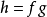
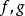



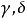

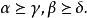
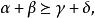

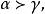


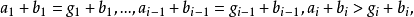

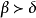

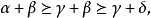



多元多項式(polynomial of several variables )是一元多項式的推廣,它是多項式理論研究的重要對象。有限多個單項式之和(假設其中不含同類項)稱為n元多項式,簡稱多項式...
在數學中,由若干個單項式相加組成的代數式叫做多項式(若有減法:減一個數等於加上它的相反數)。多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就...
多項式回歸,回歸函式是回歸變數多項式的回歸。多項式回歸模型是線性回歸模型的一種,此時回歸函式關於回歸係數是線性的。由於任一函式都可以用多項式逼近,因此多項式回歸...
多元,在社會科學中,指不同種族、民族、宗教或社會群體在一個共同文明體或共同社會的框架下,持續並自主地參與及發展自有傳統文化或利益。在多元社會中,不同族群相互...
在數學的紐結理論中,扭結多項式指的是一類以多項式表達的紐結不變數(knot invariant),而此類多項式的係數則表示它所代表的紐結的一些性質。...
研究一個因變數、與兩個或兩個以上自變數的回歸。亦稱為多元線性回歸,是反映一種現象或事物的數量依多種現象或事物的數量的變動而相應地變動的規律。建立多個變數...
代數學研究的基本對象之一。設 P 是一個數域,x 是一個文字。形式表達式稱為係數在數域 P 上 x 的一元多項式,或稱數域 P 上的一元多項式。 ...
本書包括多元線性正運算元逼近、多元插值、多元chebyshev逼近、多元校條函式、正交小波等內容。本書在注重對多元逗近基本理論、基本方法講解的同時,還力圖反映多元逗近...
多元時間序列分析(multivariate time series analysis)是指對多變數時間序列的研究。實際中,許多問題不僅是觀察單個過程xt,而且是同時觀察多個過程x1t,x2t,…,xrt,...
多元統計分析是從經典統計學中發展起來的一個分支,是一種綜合分析方法,它能夠在多個對象和多個指標互相關聯的情況下分析它們的統計規律,很適合農業科學研究的特點。...
《多項式代數》是2011年高等教育出版社出版的圖書,作者是王東明。...... 2.4 多元結式與結式系統2.5 多項式方程組求解第三章 計算交換代數與代數幾何...
《多項式代數》是2011年高等教育出版社出版的圖書,作者是王東明。...... 2.4 多元結式與結式系統2.5 多項式方程組求解第三章 計算交換代數與代數幾何...
5.3多項式回歸 5.4一次回歸的正交設計 5.5二次回歸的正交組合設計 5.6二次回歸的旋轉組合設計 習題5 第6章多元聚類與判別 6.1聚類的根據 6.2系統...
最小平方逼近多項式(polynomials of least square approximation)是一種逼近多項式,指最佳均方逼近中,取逼近函式類為多項式集合Hn時的多項式。...
在沃爾什逼近中,人們關心的是n階沃爾什多項式對函式f的最佳逼近En(f)收斂於零的速度與函式f(x)的構造性之間的關係。...
7. 多項式函式 8. 復係數與實係數多項式的因式分解 9. 有理係數多項式 10. 多元多項式 11. 對稱多項式 12. 綜合提高題型 第二章 行列式 1. n階行列式的定義...
阿廷定理(Artin theorem)實閉域上的多元多項式的重要定理.希爾伯特第17問題的正面解答和推廣.設F是一個實閉域,n為任一自然數,f(x)若對於F中任何一組元(a aZ...
整式有包括單項式(數字或字母的乘積,或者是單獨的一個數字或字母)和多項式(若干個單項式的和)。 1.單項式 沒有加減運算的整式叫做單項式。 單項式的係數:單項式中的...
