四垂心共線

四垂心共線

作者:夏培貴

引理

如圖 1（1）、（2），若AD∥BE，BD∥CE，且AD/BE=BD/CE，則A、B、C三點共線。 這不會有異議，就免去論證。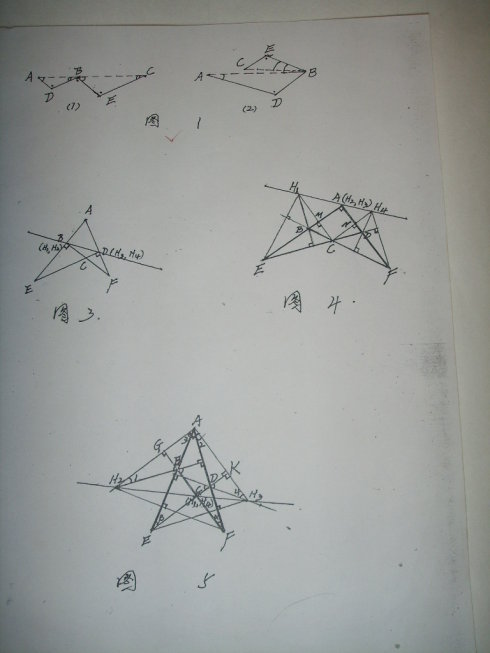

圖1,圖3,圖4,圖5

定理

完全四邊形中的四個三角形的垂心在同一條直線上。　　

證明

如圖 2（1）、（2）、（3），設完全四邊形ABCDEF中，△BCE、△ABF、△ADE、△DCF的垂心線依次為H1、H2、H3、H4；CH1交BH2、EH3於M、P；CH4交FH2、DH3於N、Q。由條件易知BH2∥EH3∥CH4，CH1∥FH2∥DH3，BH1∥AH3∥FH4，EH1∥AH2∥DH4。從而△BMC∽△CNF，△BH1M∽△H4FN。　　∴ BM/CN=MC/NF， BM/NH4=MH1/NF。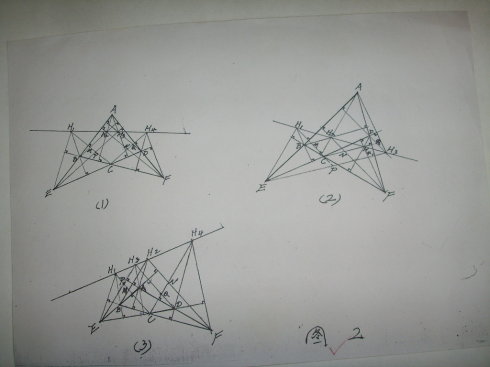

圖2

∴ NH4·MH1=CN·MC（=BM·NF）。

∴ MH1/MC=CN/NH4。

∵ MC=NH2，CN=MH2，

∴ MH1/NH2=MH2/NH4。

而MH1∥NH2，MH2∥NH4。根據引理：

H1、H2、H4共線，H2在直線H1H4上。 （一）

又 △EPC∽△CQD，△EPH1∽△H4QD。

∴ CP/DQ=EP/CQ， PH1/DQ=EP/QH4。

∴ PH1·QH4=CP·CQ（=DQ·EP）。

∴ PH1/CP=CQ/QH4。

∵ CP=QH3，CQ=PH3，

∴ PH1/QH3=PH3/QH4。

而PH1∥QH3，PH3∥QH4。根據引理：

H1、H3、H4共線，H3在直線H1H4上。 （二）

由（一）和（二）可知：H1、H2、H3、H4共線。

四垂心共線特殊情形

情形1

當AE⊥BF、AF⊥DE時，如圖3，H1、H2重合於D，B、D兩點當然在同一條直線上。

情形2

當∠A為直角時，如圖4，H2、H3重合於A，可仿前面結論（一）的證法證明H1、A、H4在同一條直線上。

情形3

當BF⊥DE時，如圖5，H1、H4重合於C。由條件易知AH2∥EK，AH3∥FG，且四邊形AGCK有三個直角，故為矩形。

證明：

由∠1=∠α=∠2，∠BGH2=∠DKA=90°及∠3=∠β=∠4，∠AGB=∠H3KD=90°，可知△BGH2∽△DKA及△ABG∽△H3DK。

∴ GH2/AK=BG/DK，AG/KH3=BG/DK。

∴ GH2/AK=AG/KH3。

∵ AK=GC，AG=KC，

∴ GH2/GC=KC/KH3，即 GH2/KC=GC/KH3。

而GH2∥KC，GC∥KH3。根據引理：

H2、C、H3共線。

綜上所述可得：完全四邊形中的四個三角形的垂心在同一條直線上。