基本介紹
定義,示例,圖表中數據,箱形圖中數據,用途,相關條目,四分位數,百分位數,
定義
四分位距通常是用來構建箱形圖，以及對機率分布的簡要圖表概述。對一個對稱性分布數據（其中位數必然等於第三四分位數與第一四分位數的算術平均數），二分之一的四分差等於絕對中位差（MAD）。中位數是集中趨勢的反映。
公式：IQR = Q3 − Q1
示例
圖表中數據
數列 | 參數 | 四分差 |
1 | 102 | |
2 | 104 | |
3 | 105 | Q1 |
4 | 107 | |
5 | 108 | |
6 | 109 | Q2 (中位數) |
7 | 110 | |
8 | 112 | |
9 | 115 | Q3 |
10 | 118 | |
11 | 118 |
從這個表格中，我們可以算出四分差的距離為 115− 105 = 10。
箱形圖中數據
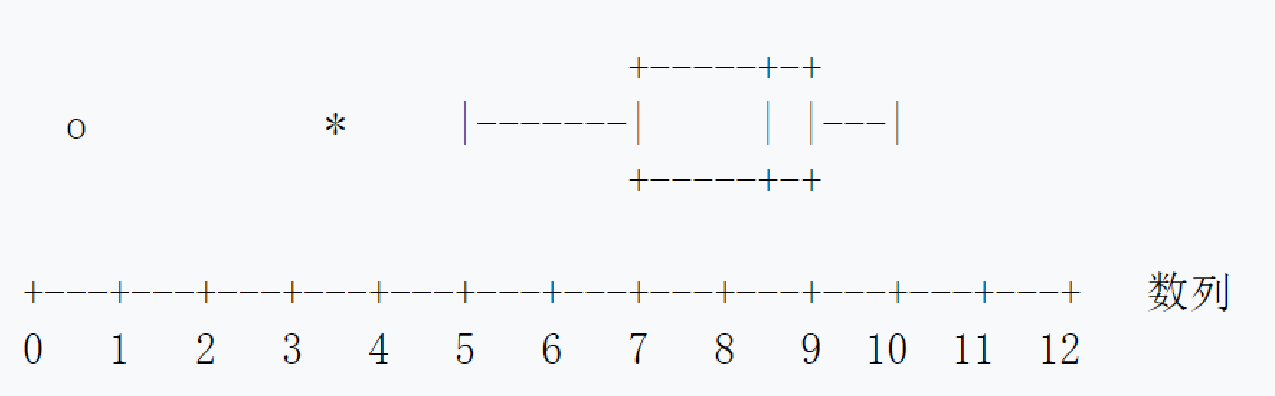圖1.箱形圖中的數據從該圖中我們可算出:
第一四分位數 (
) = 7；
中位數 (第二四分位數) (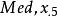
) = 8.5；
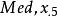
第三四分位數 (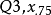
) = 9；
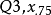
四分位距 
=Q3-Q1=2}；
四分位差 
=(Q3-Q1)/2=1}。
用途
- 與總範圍不同，四分位數範圍的分解點為25%，因此通常優選總範圍。
- IQR用於構建箱形圖，機率分布的簡單圖形表示。
- 對於對稱分布（其中中位數等於midhinge，第一和第三四分位數的平均值），IQR的一半等於中值絕對偏差（MAD）。
- 中位數是集中趨勢的相應度量。
- IQR可以用來識別異常值。
- 四分位數偏差或半四分位數範圍被定義為IQR的一半。
相關條目
四分位數
- 第一四分位數(Q1)，又稱“較小四分位數”，等於該樣本中所有數值由小到大排列後第25%的數字。
- 第二四分位數(Q2)，又稱“中位數”，等於該樣本中所有數值由小到大排列後第50%的數字。
- 第三四分位數(Q3)，又稱“較大四分位數”，等於該樣本中所有數值由小到大排列後第75%的數字。
第三四分位數與第一四分位數的差距又稱四分位距（InterQuartile Range, IQR）。
