基本介紹
- 中文名:單群
- 外文名:simple group
- 學科:數理科學
- 相關定義:商群、合成列
定義
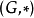
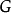

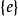
例子
有限單群
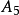

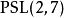
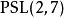

無限階單群
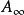
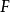
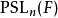
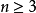
分類
有限單群
有限單群的結構
群的非單性判據
重要性
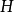
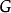
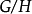
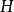
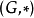
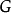

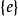
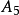

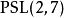
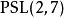

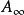
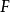
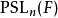
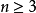
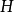
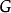
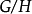
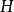
數學上的單群(英語:Simple group)是指沒有非平凡正規子群的群。任意一個群如果不是單群,都可以作進一步分解而得到一個非平凡正規子群及對應的商群。這個過程...
對於一個有限群G,當g為群G的任意元素,用g來左乘(例如若對A,就意味著gA)每一個元素的結果組成的集合與用g右乘(如Ag)每一個元素的結果組成的集合總是相同的...
有限單群的分類是代數學裡的一個巨大的工程。有限單群是除了單位元群和它本身以外沒有其他正規子群的有限群。有限單群類似於整數中的素數,可比喻為搭成有限群...
擬單群(quasisimple group)較單群更廣的一類群.設G是有限群,若G等於它的導出群,並且G/Z(G)為單群,則稱G為擬單群。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它...
《關於若干有限單群的子群體系》是由李尚志編寫,曾肯成指導的論文。...... 《關於若干有限單群的子群體系》是由李尚志編寫,曾肯成指導的論文。副題名...
1. 有限單群的數量刻畫 .國家圖書館[引用日期2014-07-30] 詞條標籤: 文學作品 , 文化 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:3次歷史版本 最近更新...
《半單群的表示論》是由2011年世界圖書出版公司出版的圖書,作者是納普。本書分為上下兩卷,前十章為上卷,後六章為下卷。書中講述半單李群表示理論的方式給出了...
單群擴張塔(extension tower with simplegroups)一種與根式擴域相關的域擴張.它與方程有無根式解有密切關係.設K是域F的擴域,若存在一個子域鏈:使得G <K1/K2...
有限群是具有有限多個元素的群。群論的重要內容之一。其所含元素的個數,稱為有限群的階。有限群可分為兩大類:可解群與非可解群(特別包括非交換單群)(見群...
魔群(Monster Group)是最大的散在單群。...... 事實上,早在1976年,格瑞斯在《大魔單群的結構》 [4] 一文中曾指出滿足前麵條件的群G(稱為F1型群或大魔群...
