基本介紹
- 中文名:判定器
- 外文名:Sipser
- 性質:圖靈機的一種
- 領域:計算機
簡介
全圖靈機可計算的函式
與偏圖靈機的關係
- 所有用偏圖靈機可計算的偏函式都可以被擴展(就是說擴大它的定義域)成為全可計算函式嗎?
- 有可能改變圖靈機的定義使得特定類的全圖靈機計算所有全可計算函式?
- 定理。有不能擴展成全圖靈機可計算函式的圖靈可計算偏函式。特別是偏函式f,它被定義得使f(n) =m,若且唯若帶有附標n的圖靈機停機於輸入0並輸出m,它沒有到全可計算函式的擴展。
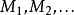
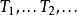

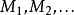
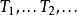

在可計算性理論中,總是停機的機器也叫做判定器(Sipser,1996年)或全圖靈機(Kozen,1997年)是對所有輸入總是停機的圖靈機。...
檢測器指能檢測色譜柱流出組分及其量的變化的器件。檢測器通常分為積分型和微分型兩類。對檢測器的要求是:靈敏度高,線性範圍寬,重現性好,穩定性好,回響速度快,...
檢驗器是一類用來為檢測某一物殊物質而設計製作的物品的總稱。...... 檢驗器是一類用來為檢測某一物殊物質而設計製作的物品的總稱。有關產品雙張檢測器 氣體檢測...
特徵檢測器發明提供了一種車輛動態特性檢測器(10),其用於從自主感測器(13至16)獲得檢測信息,以檢測車輛動態特性的變化。...
車輛檢測器,更標準的稱謂應該是:交通信息檢測器。目前國內外在交通檢測系統或交通信息採集系統中,大量套用了電磁感測技術、超聲感測技術、雷達探測技術、視頻檢測技術...
二極體陣列檢測器(又稱DAD檢測器)是一種基於光電二極體陣列技術的新型檢測器。使用二極體陣列檢測器,可以對色譜峰進行光譜掃描、峰純度鑑定等定性分析,在方法研究中...
電子捕獲檢測器(electron capture detector),簡稱ECD。 電子捕獲檢測器也是一種離子化檢測器,它是一個有選擇性的高靈敏度的檢測器,它只對具有電負性的物質,如含...
環境檢測器是指用於檢測道路上的雨、霧、冰、雪,或隧道中一氧化碳含量等影響交通安全的氣象條件的檢測器。一旦檢測到有害的環境條件,環境檢測器就驅動交通信號或...
行人檢測器編輯 鎖定 本詞條由“科普中國”百科科學詞條編寫與套用工作項目 審核。行人檢測儀是利用計算機視覺技術判斷圖像或者視頻序列中是否存在行人並給予精確...
氣相檢測器操作過程中在色譜柱後增加一路載氣直接進入檢測器,就可保證檢測器在高靈敏度狀態下工作。...
電子俘獲檢測器(ecd)是靈敏度最高的氣相色譜檢測器,同時又是最早出現的選擇性檢測器。它僅對那些能俘獲電子的化合物,如鹵代烴、含 n、o和 s等雜原子的化合物...
微軟在以Windows NT為核心的作業系統中都集成有事件查看器,它是 Microsoft Windows 作業系統工具。事件查看器是重要的系統管理軟體。...
螢光檢測器(Fluorescence Detector,簡稱FLD)是高壓液相色譜儀常用的一種檢測器。用紫外線照射色譜餾分,當試樣組分具有螢光性能時,即可檢出。...
紅外檢測器可用來測定附近有沒有如手持遙控器等發射出的調製紅外線,紅外檢測就是利用紅外輻射原理對設備或材料及其它物體的表面進行檢驗和測量的專門技術,也是採集...
查看器是一款系統安全類軟體,支持Android 1.6。...... 圖集 查看器圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:一謎佢...
包括:殼體,在該殼體的表面設定有功能鍵,所述功能鍵與微處理器相連,所述微處理器分別與唯讀存儲器、顯示器、發光二極體相連,其特徵在於,在殼體內設有檢測盒,盒內...
