發明者 1936年,
艾倫·圖靈 (1912-1954)提出了一種抽象的計算模型 —— 圖靈機 (Turing Machine)。
圖靈機的藝術表示 基本思想 圖靈的基本思想是用機器來模擬人們用紙筆進行數學運算的過程,他把這樣的過程看作下列兩種簡單的動作:
圖靈機 在紙上寫上或擦除某個符號;
把注意力從紙的一個位置移動到另一個位置;
而在每個階段,人要決定下一步的動作,依賴於 (a) 此人當前所關注的紙上某個位置的符號和(b) 此人當前思維的狀態。
為了模擬人的這種運算過程,圖靈構造出一台假想的機器,該機器由以下幾個部分組成:
1.一條無限長的紙帶 TAPE 。紙帶被劃分為一個接一個的小格子,每個格子上包含一個來自有限字母表的符號,字母表中有一個特殊的符號 表示空白。紙帶上的格子從左到右依此被編號為 0,1,2,... ,紙帶的右端可以無限伸展。
2.一個讀寫頭 HEAD 。該讀寫頭可以在紙帶上左右移動,它能讀出當前所指的格子上的符號,並能改變當前格子上的符號。
3.一套控制規則 TABLE 。它根據當前機器所處的狀態以及當前讀寫頭所指的格子上的符號來確定讀寫頭下一步的動作,並改變狀態暫存器的值,令機器進入一個新的狀態。
4.一個
狀態暫存器 。它用來保存圖靈機當前所處的狀態。圖靈機的所有可能狀態的數目是有限的,並且有一個特殊的狀態,稱為停機狀態。參見
停機問題 。
注意這個機器的每一部分都是有限的,但它有一個潛在的無限長的紙帶,因此這種機器只是一個理想的設備。圖靈認為這樣的一台機器就能模擬人類所能進行的任何計算過程。
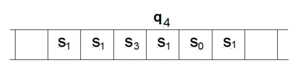
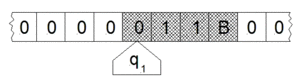
在某些模型中,讀寫頭沿著固定的紙帶移動。要進行的指令(q1)展示在讀寫頭內。在這種模型中“空白”的紙帶是全部為 0 的。有陰影的方格,包括讀寫頭掃描到的空白,標記了 1,1,B 的那些方格,和讀寫頭符號,構成了系統狀態。(由 Minsky (1967) p.121 繪製)。
形式化 一台圖靈機是一個七元組,{Q,Σ,Γ,δ,q0,qaccept,qreject},其中 Q,Σ,Γ 都是有限集合,且滿足
1.Q 是狀態集合;
2.Σ 是輸入字母表,其中不包含特殊的空白符 □;
3.Γ 是帶字母表,其中 □∈Γ且Σ∈Γ ;
4. δ:Q×「→Q×Γ×{L,R}是轉移函式,其中L,R 表示讀寫頭是向左移還是向右移;
5.q0∈Q是起始狀態;
6. qaccept是接受狀態。
7.qreject是拒絕狀態,且。qreject≠qaccept
圖靈機 M = (Q,Σ,Γ,δ,q0,qaccept,qreject) 將以如下方式運作:
開始的時候將輸入符號串 從左到右依此填在紙帶的第 號格子上, 其他格子保持空白(即填以空白符)。M 的讀寫頭指向第 0 號格子, M 處於狀態 q0。機器開始運行後,按照轉移函式 δ 所描述的規則進行計算。例如,若當前機器的狀態為 q,讀寫頭所指的格子中的符號為 x, 設 δ(q,x) = (q',x',L), 則機器進入新狀態 q', 將讀寫頭所指的格子中的符號改為 x', 然後將讀寫頭向左移動一個格子。若在某一時刻,讀寫頭所指的是第 0 號格子, 但根據轉移函式它下一步將繼續向左移,這時它停在原地不動。換句話說,讀寫頭始終不移出紙帶的左邊界。若在某個時刻 M 根據轉移函式進入了狀態 qaccept, 則它立刻停機並接受輸入的字元串; 若在某個時刻 M 根據轉移函式進入了狀態 qreject, 則它立刻停機並拒絕輸入的字元串。
注意,轉移函式 δ 是一個部分函式, 換句話說對於某些 q,x, δ(q,x) 可能沒有定義, 如果在運行中遇到下一個操作沒有定義的情況, 機器將立刻停機。
停機問題 停機問題(halting problem)是目前邏輯數學的焦點,和
第三次數學危機 的解決方案。其本質問題是: 給定一個圖靈機 T,和一個任意語言集合 S,是否 T 會最終停機於每一個。其意義相同於可確定語言。顯然任意有限 S 是可判定性的,可數的(countable) S 也是可停機的,在使用 oracle 輸入的幫助下。
通俗的說,停機問題就是判斷任意一個程式是否會在有限的時間之內結束運行的問題。如果這個問題可以在有限的時間之內解決,可以有一個程式判斷其本身是否會停機並做出相反的行為。這時候顯然不管
停機問題 的結果是什麼都不會符合要求。所以這是一個不可解的問題。
停機問題本質是一階邏輯的不自恰性和不完備性。類似的命題有理髮師悖論、全能悖論等。
證明:
設停機問題有解,即:存在過程H(P,I)可以給出程式P在輸入I的情況下是否可停機。假設若P在輸入I時可停機,H輸出“停機”,反之輸出“死循環”,即可導出矛盾:
顯然,程式本身可以被視作數據,因此它可以被作為輸入,故H應該可以判定當將P作為P的輸入時,P是否會停機。所以我們設過程K(P)的流程如下:首先,它調用H(P,P),如果H(P,P)輸出“死循環”,則K(P)停機,反之K(P)死循環。即K(P)做與H(P,P)的輸出相反的動作。
現在假設求K(K),則若H(K,K)輸出停機,K(K)死循環,但由定義知二者矛盾。反之,H(K,K)輸出死循環,則K(K)停機,兩者一樣矛盾。
因此,H不是總能給出正確答案,故而不存在解決停機問題的方法。
通用機型 對於任意一個圖靈機,因為它的描述是有限的,因此我們總可以用某種方式將其編碼為字元串。我們用 <M> 表示圖靈機 M 的編碼。
我們可以構造出一個特殊的圖靈機,它接受任意一個圖靈機 M 的編碼<M> ,然後模擬 M 的運作,這樣的圖靈機稱為
通用圖靈機 (Universal Turing Machine)。現代電子計算機其實就是這樣一種通用圖靈機的模擬,它能接受一段描述其他圖靈機的程式,並運行程式實現該程式所描述的
算法 。但要注意,它只是模擬,因為現實中的計算機的存儲都是有限的,所以無法跨越
有限狀態機 的界限。
變體 圖靈機有很多變種,但可以證明這些變種的計算能力都是等價的,即它們識別同樣的語言類。證明兩個計算模型 A 和 B 的計算能力等價的基本思想是:用 A 和 B 相互模擬, 若 A 可模擬 B 且 B 可模擬 A, 顯然他們的計算能力等價。注意這裡我們暫時不考慮計算的效率,只考慮計算的理論上“
可行性 ”。
首先我們可以發現,改變圖靈機的帶字母表並不會改變其計算能力。例如我們可以限制圖靈機 的帶字母表為 {0,1},這並不會改變圖靈機的計算能力,因為我們顯然可以用帶字母表為 {0,1} 的圖靈機模擬帶字母表為任意有限集合 Γ 的圖靈機。
另一個要注意的是,如果我們允許圖靈機的紙帶兩端都可以無限伸展,這並不能增加圖靈機的計 算能力,因為我們顯然可以用只有紙帶一端能無限伸展的圖靈機來模擬這種紙帶兩端都可以無限 伸展的圖靈機。
如果我們允許圖靈機的讀寫頭在某一步保持原地不動,那也不會增加其計算能力,因為我們可以用 向左移動一次再向右移動一次來代替在原地不動。
其它的常見圖靈機變種包括:
多帶圖靈機
可計算性 圖靈可判定語言
遞歸可枚舉語言
停機問題
可判定性
不可判定性
等價機器 除了圖靈機以外,人們還發明了很多其它的計算模型。包括:
然而這些模型無一例外地都和圖靈機的計算能力等價,因此邱奇,圖靈和
哥德爾 提出了著名的邱奇-圖靈論題:一切直覺上能行可計算的函式都可用圖靈機計算,反之亦然。
 圖靈機的藝術表示
圖靈機的藝術表示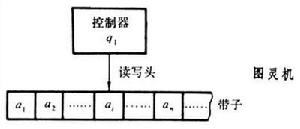 圖靈機
圖靈機