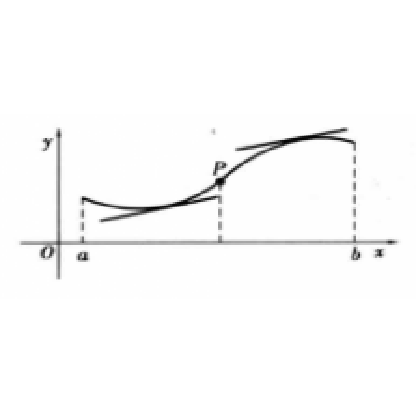
曲線的凹或凸統稱為曲線的凸性。
從切線角度講,下凸弧上過任一點的切線都在曲線弧之下,而上凸弧上過任一點的切線都在曲線弧之上。
從割線角度講,如果連續曲線y=f(x)在區間(a,b)對應的曲線弧上任意兩點的割線線段都在該兩點間的曲線弧之上,則稱該段曲線弧是下凸的,並稱函式y=f(x)在區間(a,b)上是下凸的(或上凹的,即曲線開口向上)。如果連續曲線y=f(x)在區間(a,b)對應的曲線弧上任意兩點的割線線段都在該兩點間的曲線弧之下,則稱該段曲線弧是上凸的,並稱函式y=f(x)在區間(a,b)上是上凸的(或下凹的,即曲線開口向下)。
從導數角度講,設y=f(x)在(a,b)內具有二階導數,如果在(a,b)內f''(x)>o,則y=f(x)在(a,b)內為下凸;如果在(a,b)內f''(x)<o,則y=f(x)在(a,b)內為上凸。
基本介紹
- 中文名:凸性
- 外文名:convexity
- 所屬學科:數理科學
- 分類:曲線的凹或凸統稱為曲線的凸性
意義
基本概念
凹函式和凸函式
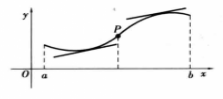 圖1
圖1凸性的定義
判斷曲線的凸性













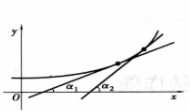 圖2
圖2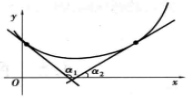 圖3
圖3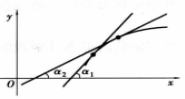 圖4
圖4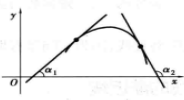 圖5
圖5例題解析






x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
y'' | + | 0 | - | 0 | + |
y | ∪ | 拐點 | ∩ | 拐點 | ∪ |






x | (-∞,2) | 2 | (2,+∞) |
y'' | - | 不存在 | + |
y | ∩ | 拐點 | ∪ |