基本介紹
- 中文名:全序集
- 外文名:totally ordered set
- 別名:鏈、全有續集、線性有序集
- 所屬領域:數學
- 表達式:(A,≤)
定義
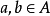













良序集與全序集
定理1




定理2




例題解析






常見全序集






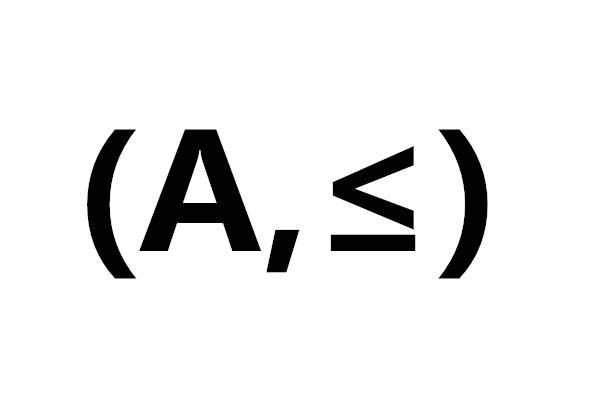
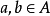














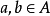



















設(A,≤)是偏序集,如果(A,≤)中的關係“≤”滿足條件:對於任意的a,b∈A,a≤b或b≤a至少有一個成立,那么就稱關係≤為序關係,稱A為在這個關係下的全序...
可分全序集(separable totally ordered set)一種重要的全序集.指有一個可數稠密子集的全序集.因為有理數集是實數集的可數稠密子集,所以實數集是可分的. ...
在數學中,集合 X 上的全序關係(Total order),簡稱全序、又名線性序(linear order)、簡單序(simple order),或(非嚴格)排序((non-strict) ordering),是在 X...
這個偏序是全序。整數的集合配備了它的自然次序。這個偏序是全序。自然數的集合的有限子集 {1, 2, ..., n}。這個偏序是全序。自然數的集合配備了整除關係...
嚴格全序關係(strictly totally ordered rela-tion)亦稱嚴格線性序關係、嚴格有序關係一種重要的全序關係.指集合A上的不對稱的、傳遞的、弱連通的二元關係R. A稱...
定義 全序半環(total ordered semirings)一類重要的半環.一個半群(S,·)稱為全序半群,是指<S,鎮)做成全序集,並且,對S中任意元素二,y,若二鎮y,則對...
全序集中的關係≤稱為全序或線性序。若偏序集P的子集C作為子偏序集是全序集,則稱C是P中的鏈;若C是非序的,則稱C為P的反鏈。實數集及其任何子集在通常的...
設集合(S,≤)為一全序集,≤是其偏序關係,若對任意的S的非空子集,在其序下都有最小元素,則稱≤為良序關係,(S,≤)為良序集。...
若集合S上定義了一個偏序,則S稱為偏序集(poset);若將其上的偏序關係改為其逆關係,得到的新偏序集S'稱為S的序對偶。雖然通常術語“有序集”用來稱呼全序集,...
給定帶有偏序≤的一個集合S,無窮降鏈是鏈V,就是說在其上≤定義了全序的S的子集,使得V沒有最小元素,也就是元素m它使得對於在V中所有元素n有著m ≤ n。....
給定帶有偏序≤的一個集合S,無窮降鏈是鏈V,就是說在其上≤定義了全序的S的子集,使得V沒有最小元素,也就是元素m它使得對於在V中所有元素n有著m≤n。...
全序集是一棵偽樹,並且它的枝疊合在一起,偏序結構〈A,R〉成為偽樹時,其哈塞圖在直觀上像一棵或多棵分離開的樹,只有向上的分叉,而無向下的分叉,並且無閉合...
2.序結構:由集合及其上的序關係組成,如偏序集、全序集、良序集。3.拓撲結構:由集合及其上的拓撲組成,如拓撲空間、度量空間、緊緻集、列緊空間等。...
在序理論中,不限制於實數集合,可以考慮任意偏序集合甚至是預序集合。在這些情況下上述定義同樣適用。但是要避免術語"遞增"和"遞減",因為一旦處理的不是全序的次序...
濾子基(filter base)生成濾子的一類集族。在數學中,濾子是偏序集合的特殊子集。經常使用的特殊情況是:要考慮的有序集合只是某個集合的冪集,並用集合包含來排序...
2.7.3全序集與良序集習題2第3章函式3.1函式的基本概念3.2特殊函式3.3複合函式與逆函式3.3.1複合函式3.3.2逆函式習題3第4章命題邏輯...
集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。...
序拓撲(order topology)在全序集(線性序集)上依序關係定義的一類拓撲.設(X,)為全序集,則以所有形如{.x } .xGa }與{.x } .x } a }的集合為子基在...
誠然,在《關於素性環》一文中,他證明了一個整環的所有理想都是素性理想(這種環稱為素性環),其充要條件是其所有素理想的集按包含關係組成一個全序集。這...
設集合 (S ,≤) 為一全序集,≤是其偏序關係。對任意 的S 的非空子集都有在其序下有最小元素,則稱≤為良序關係,(S ,≤) 為良序集。...
格序單群(lattice-ordered simple group)亦稱L單群。是單群在格序群範疇中的推廣。沒有真L理想的格序群稱為格序單群或L單群。若全序集T是2齊次的,則A(T...
有序域是具有全序關係,且序關係滿足一定規律的域。偏序集的概念(參看“偏序關係”)可以推廣到代數繫上討論,可以定義偏序群及偏序環等概念。若<G,·>是群,且<...
由偏序集P按如下方式產生的圖G稱為偏序集的可比圖:G的節點集由P的元素組成,而e為G中的邊,僅當e的兩端點在P中是可比較的,有限全序集的可比圖為完全圖 [...
