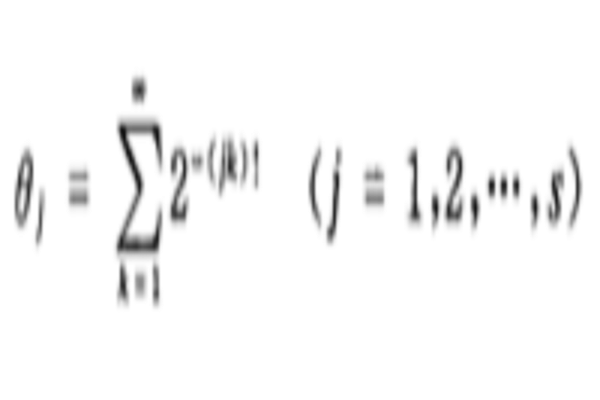代數無關性(algebraic independence offields over a given field)是元素的代數無關性概念到域的開拓。設M是域F的擴域,K,I為其兩個中間域,若K的任意一個在F上代數無關的子集也在I上代數無關(或等價地說,I的任意一個在F上代數無關的子集也在K上代數無關),則稱K與I在F上代數無關。
基本介紹
- 中文名:代數無關性
- 外文名:algebraic independence offields over a given field
- 所屬學科:數理科學
- 相關概念:超越數論
- 主要問題:確定幾個數的代數無關性
歷史,數的代數無關性,對數代數無關性,指數的代數無關性,
歷史
Gel’fond-Schneider定理給出了 的超越性,其中α≠0,1是代數數,β是次數為d>1的代數數.1948年A.0.Gel’fond提出了
的超越性,其中α≠0,1是代數數,β是次數為d>1的代數數.1948年A.0.Gel’fond提出了 ,
, ,…,
,…, 的代數無關性問題.他證明了:若β是三次代數數,則
的代數無關性問題.他證明了:若β是三次代數數,則 ,
, 是代數無關的.他還宣布:一般地,當d≥2時,
是代數無關的.他還宣布:一般地,當d≥2時, ,
, ,…,
,…, 中至少有[(d+1)/2]個數是代數無關的,但沒有給出證明.直到1987年,人們改進和推廣了Gel’fond—Schneider方法才證明了這個結論.1971年,R.Tijdemann套用Gel’fond.Schneider方法證明了數e,π,eˆπ,
中至少有[(d+1)/2]個數是代數無關的,但沒有給出證明.直到1987年,人們改進和推廣了Gel’fond—Schneider方法才證明了這個結論.1971年,R.Tijdemann套用Gel’fond.Schneider方法證明了數e,π,eˆπ, 中至少有兩個是代數無關的.1996年,Yu.V.Nesterenko證明了π,eˆπ,Γ(1/4)是代數無關的.他在證明中套用了來自交換代數和代數幾何的技術,提出一種新的代數無關性證明方法,並將其用於其他代數無關性問題.這是當代超越數論的最重要的進展.人們推測他的方法(或其改進形式)有可能給出更多的代數無關性結果.例如,人們猜測:兩組數π,Γ(1/3),Γ1/4)及e,π,eˆπ,Γ(1/4)分別是代數無關的;數π,Γ(1/5),Γ(2/5)、eˆ√5π中有三個數是代數無關的;等等.值得注意的是,e和兀是否代數無關仍未解決.有一個相當弱的結果:若eˆ(π2)是代數數,則e和π代數無關.
中至少有兩個是代數無關的.1996年,Yu.V.Nesterenko證明了π,eˆπ,Γ(1/4)是代數無關的.他在證明中套用了來自交換代數和代數幾何的技術,提出一種新的代數無關性證明方法,並將其用於其他代數無關性問題.這是當代超越數論的最重要的進展.人們推測他的方法(或其改進形式)有可能給出更多的代數無關性結果.例如,人們猜測:兩組數π,Γ(1/3),Γ1/4)及e,π,eˆπ,Γ(1/4)分別是代數無關的;數π,Γ(1/5),Γ(2/5)、eˆ√5π中有三個數是代數無關的;等等.值得注意的是,e和兀是否代數無關仍未解決.有一個相當弱的結果:若eˆ(π2)是代數數,則e和π代數無關.













超越數論中不少問題都與指數函式或其反函式即對數函式有關.例如,C.L.Siegel,S.Lang及K.Ramachandra證明了下面的定理(通常稱為六指數定理):如果兩組複數x1,x2及y1,y2,y3分別在Q上線性無關,那么六個數 (i=1,2;j=1,2,3)中至少有一個超越數.若在這個定理中,取x1=1,x2=π;y1=log 2,y2 πlog 2,y3= π2log 2,則
(i=1,2;j=1,2,3)中至少有一個超越數.若在這個定理中,取x1=1,x2=π;y1=log 2,y2 πlog 2,y3= π2log 2,則 (i = 1,2;j=1,2,3)是2,2ˆπ,2ˆπ2,2ˆπ,2ˆπ2,2ˆπ3,因而我們得知:數2ˆπ,2ˆπ2,2ˆπ3中至少有一個超越數.一般地,C.L.Siegel,Th.Schneider,S.Lang及K.Ramachandra提出:
(i = 1,2;j=1,2,3)是2,2ˆπ,2ˆπ2,2ˆπ,2ˆπ2,2ˆπ3,因而我們得知:數2ˆπ,2ˆπ2,2ˆπ3中至少有一個超越數.一般地,C.L.Siegel,Th.Schneider,S.Lang及K.Ramachandra提出:


四指數猜想
如果兩組複數x1,x2及y1,y2分別在Q上是線性無關的,那么四個數 (i = 1,2;j=1,2)中至少有一個超越數.
(i = 1,2;j=1,2)中至少有一個超越數.

另一個與指數函式有關的重要猜想是: Schanuel猜想 設複數x1,…,
Schanuel猜想 設複數x1,…, 在Q上線性無關,那么2s個數x1,…,,
在Q上線性無關,那么2s個數x1,…,, ,…,
,…, 中至少有s個是代數無關的.這個猜想是由S.Schanuel提出的,並由S.Lang於1966年首先公布.
中至少有s個是代數無關的.這個猜想是由S.Schanuel提出的,並由S.Lang於1966年首先公布.




若在其中取X1=1,X2=2πi,即得猜想:e,π是代數無關的.若取s=d≥2, =(log α)βˆ(j-1)(j=1,…,d),其中α≠0,1,而β是d次代數數,log α表示α的自然對數的某個分支,可得猜想:logα,αˆβ,αˆβ2,…,αˆ(βˆ(d-1))是代數無關的.我們已由六指數定理推出數2ˆπ,2ˆπ2,2ˆπ3中至少有一個超越數,但尚不知道2ˆπ,2ˆπ2中是否有一個超越數;但若Schanuel猜想成立,則可推出π,log 2,2ˆπ,2ˆπ2,2ˆπ3代數無關.實際上,可以證明四指數猜想是Schanuel猜想的一個推論.Schanuel猜想的另外一個有趣的推論是:若它成立,則下列17個數代數無關:
=(log α)βˆ(j-1)(j=1,…,d),其中α≠0,1,而β是d次代數數,log α表示α的自然對數的某個分支,可得猜想:logα,αˆβ,αˆβ2,…,αˆ(βˆ(d-1))是代數無關的.我們已由六指數定理推出數2ˆπ,2ˆπ2,2ˆπ3中至少有一個超越數,但尚不知道2ˆπ,2ˆπ2中是否有一個超越數;但若Schanuel猜想成立,則可推出π,log 2,2ˆπ,2ˆπ2,2ˆπ3代數無關.實際上,可以證明四指數猜想是Schanuel猜想的一個推論.Schanuel猜想的另外一個有趣的推論是:若它成立,則下列17個數代數無關:

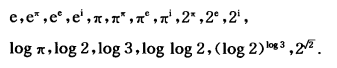
由Hermite—Lindemann定理可知,Schanuel猜想迄今只對s=1成立.一般情形的解決極為困難.另外,人們還提出Schanuel猜想的推廣形式.
當然還有許多其他超越數論猜想,如正文中提到的ζ(2k+1)(k≥1)、Catalan常數及γ常數的無理性或超越性等.
數的代數無關性
對於s個複數θ1,…,θs,若存在一個含s個變數的整係數非零多項式P(Z1,…,Zs),使得P(θ1,…,θs)=0,則稱θ1,…,θs,(在有理數域Q上)代數相關,不然稱θ1,…,θs(在有理數域Q上)代數無關.因此,若θ1,…,θz代數無關,則對任何s個變數的整係數非零多項式P(z1,…,zs),總有P(θ1,…,θs)≠0,並且θi(1≤j≤s)中的任意個也代數無關;特別地,這s個數全是超越數.例如,π和π2是代數相關的,因為它們滿足 一z2=0.可以證明:對於任何整數s≥1,實數
一z2=0.可以證明:對於任何整數s≥1,實數

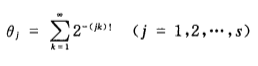
是代數無關的.
代數無關性概念的定量形式為:
設θ1,…,θs是s個複數.如果存在一個正整變數x,y的正值函式ψ(x,y),具有下列性質:對於任意給定的正整數d,H,以及任何次數≤d,高(即係數絕對值的最大值)≤H的整係數非零多項式P(z1,…,zs),有
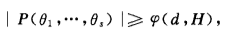
那么稱ψ(d,H)是θ1,…,θs的一個代數無關性度量.特別地,當S=1時,稱其為θ1的超越性度量.當然,這個定義蘊涵了θ1,…,θs的代數無關性(或θ1的超越性).例如,對於log 2,可取
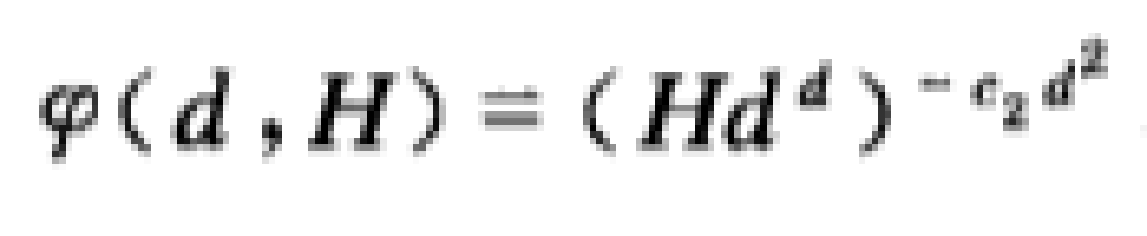
其中C2>0是一個常數,也就是說,對於任何次數≤d、高≤H的整係數非零多項式P(z),有
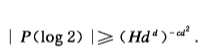
超越數論的基本任務就是確定一個數的超越性或幾個數的代數無關性(定性和定量兩個方面).
對數代數無關性
沙努爾猜想是超越數論中最基本最前沿的問題,它被認為是包含了已知的與指數(對數)函式值的超越性有關的所有結果以及所有合理的猜想.這個猜想的解決將會導致整個超越數論發生翻天覆地的改變,大部分超越數論的謎題也會隨之迎刃而解.
在提出沙努爾猜想之前首先有的是對數代數無關性猜想和根據六指數定理提出的四指數猜想.
對數代數無關性猜想:
若x1,…,xn為非零的代數數使得lgx1,…,lgxn在Q上線性無關,則lgx1,...,lgxn代數無關.對數代數無關性猜想的證明是許多數學家畢生的追求,但可惜的是我們只證明了n=1的情況,當n≥2時,我們毫無頭緒,我們連是否存在代數數x1,x2使得lgx1,lgx2代數無關都不知道.
根據兩個猜想,沙努爾提出了更一般的猜想.
沙努爾猜想:
若x1,…,xn為Q上線性無關的複數,則x1,...,Xn,eˆx1,…,eˆ(xn)這2n個數中至少有n個代數無關.我們可以分析一下這個猜想.當x1,...xn均為代數數時,這個猜想就是我們上面講述的林德曼一魏爾斯特拉斯定理.當eˆx1,…,eˆ(xn)如均為代數數時,這個猜想就變成了上面的對數代數無關性猜想了.因此,我們才會說沙努爾猜想是超越數論中所有合理猜想的“綜合”.數學家們經過努力,但只能在加上一些附加條件時才能得到證明,對於這個猜想本身,由於缺少有效的工具和方法,還看不到解決該猜想的希望.
指數的代數無關性
定理一 設複數α0,α1,α2及γ0,γ1,γ2分別Q線性無關,則數
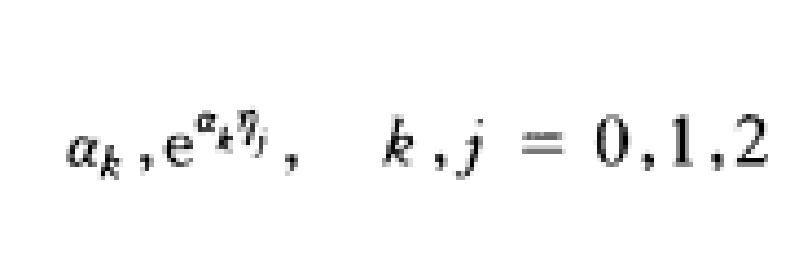
中至少有兩個代數無關.
定理2 設複數α0,α1,α2及η0,η1,分別Q線性無關,則數
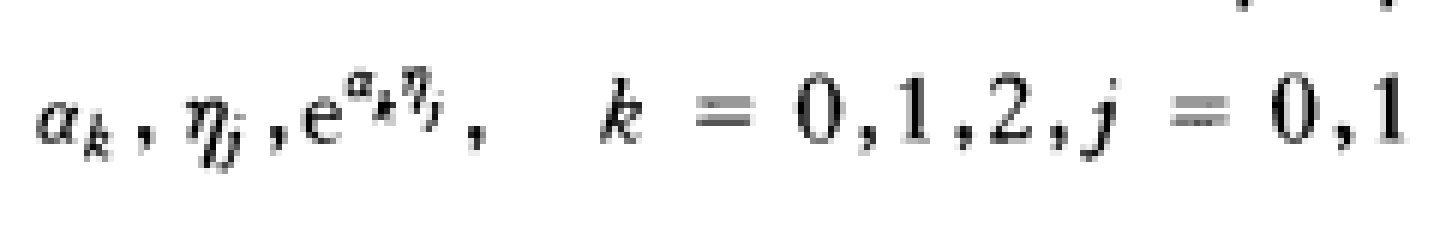
中至少有兩個代數無關.