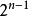主元(pivot element),一種變元。指在消去過程中起主導作用的元素。
基本介紹
- 中文名:主元
- 外文名:pivot element
- 適用範圍:數理科學
主元消去法,部分主元高斯消去法,全主元高斯消去法,套用,
主元消去法
[pivoting elimination method]
高斯消去法在消元過程中可能出現零主元,即 ,這時消元過程將無法進行;也可能主元
,這時消元過程將無法進行;也可能主元 ,但其絕對值非常小,用它做除法將會導致捨入誤差的擴散,使數值解不可靠。解決該問題的辦法是避免使用絕對值過小的元素作主元。選主元早在1947年就已由馮·諾依曼(von Neumann)和戈爾德施泰因(Goldstine)所使用。
,但其絕對值非常小,用它做除法將會導致捨入誤差的擴散,使數值解不可靠。解決該問題的辦法是避免使用絕對值過小的元素作主元。選主元早在1947年就已由馮·諾依曼(von Neumann)和戈爾德施泰因(Goldstine)所使用。


在第 k 步消元時,通常採用如下方式選取主元:在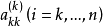 中選擇絕對值最大者作為主元;或在
中選擇絕對值最大者作為主元;或在 中選擇絕對值最大者作為主元。前者被稱為部分主元(partial pivoting)或列主元,後者則被稱為全主元(complete pivoting)。術語“部分主元”和“全主元”由威爾金森(Wilkin-son)所提出。
中選擇絕對值最大者作為主元。前者被稱為部分主元(partial pivoting)或列主元,後者則被稱為全主元(complete pivoting)。術語“部分主元”和“全主元”由威爾金森(Wilkin-son)所提出。
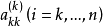

部分主元高斯消去法
部分主元高斯消去法消元過程的第 k 步如下:
(1)選主元,選取 作為主元。若
作為主元。若 有多個值,則取
有多個值,則取 中最小者;
中最小者;



(2)交換 的第 k ,
的第 k , 行,並將交換之後的增廣矩陣仍記為
行,並將交換之後的增廣矩陣仍記為 ;
;



(3)將 第 k 行的
第 k 行的 倍加到第i=(i=k=1,...,n)行。
倍加到第i=(i=k=1,...,n)行。


經過 步消元,得到
步消元,得到 ,其中
,其中 是上三角矩陣,則Ax=b化為一個同解上三角方程組,套用回代法即可求得方程組的解。部分主元高斯消去法的工作量約為
是上三角矩陣,則Ax=b化為一個同解上三角方程組,套用回代法即可求得方程組的解。部分主元高斯消去法的工作量約為 個浮點運算和
個浮點運算和 次邏輯運算。
次邏輯運算。





也可以用矩陣運算表示部分主元高斯消去法的消元過程。交換單位矩陣 I 的第 i ,j(i < j)兩行(列)所得的矩陣被稱為初等置換矩陣,記為 ,簡記為
,簡記為 ,則
,則 是對稱正交矩陣。設第 k 步中交換
是對稱正交矩陣。設第 k 步中交換 第 k,
第 k, 行的初等置換矩陣為
行的初等置換矩陣為 ,高斯變換矩陣為
,高斯變換矩陣為 。記
。記
 ,
,
 則可以證明:P 是排列矩陣,並且PA=LU。因此,矩陣 A 的部分主元消元過程實現了 A 的一個部分主元三角分解。
則可以證明:P 是排列矩陣,並且PA=LU。因此,矩陣 A 的部分主元消元過程實現了 A 的一個部分主元三角分解。











全主元高斯消去法
全主元高斯消去法消元過程的第 k 步如下:
(1)選主元,選取 作為主元。若
作為主元。若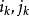 有多少個值,則分別取
有多少個值,則分別取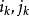 中最小者;
中最小者;

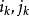
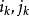
(2)交換 的第 k ,
的第 k , 行和第
行和第 列,並將交換之後的增廣矩陣仍記為
列,並將交換之後的增廣矩陣仍記為 ;
;




(3)將 第 k 行的
第 k 行的 倍加到第
倍加到第 行。
行。



經過 步消元,得到數組
步消元,得到數組 和
和 ,其中
,其中 是該上三角矩陣。套用回代法即可求得上三角方程組的解,利用數組
是該上三角矩陣。套用回代法即可求得上三角方程組的解,利用數組 可得到原方程的解。
可得到原方程的解。





全主元高斯消去法的工作量約為 個浮點運算和
個浮點運算和 次邏輯運算。與部分主元高斯消去法相比,全主元高斯消去法在其每步的兩維數組搜尋時需要增加很大的選主元工作量。
次邏輯運算。與部分主元高斯消去法相比,全主元高斯消去法在其每步的兩維數組搜尋時需要增加很大的選主元工作量。


全主元高斯消去法的消元過程也可用矩陣運算表示。設第 k 步中交換 的第
的第 行的初等置換矩陣為
行的初等置換矩陣為 ,交換
,交換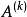 的第
的第 列第初等置換矩陣為
列第初等置換矩陣為 ,高斯變換矩陣為
,高斯變換矩陣為 。記
。記
 ,
, ,
, ,則可以證明:P,Q是排列矩陣,並且PAQ=LU。因此,矩陣 A 的全主元消元過程實現了 A 的一個全主元三角分解。
,則可以證明:P,Q是排列矩陣,並且PAQ=LU。因此,矩陣 A 的全主元消元過程實現了 A 的一個全主元三角分解。










套用
在20世紀40年代中期,馮·諾依曼等預言高斯消去法一定是數值不穩定的。在20世紀50年代早期,計算經驗已經證實主元高斯消去法實際上是穩定的。對這種現象的解釋在理論上是一個很大的挑戰。威爾金森因對這個課題的貢獻而成名。可以證明:如果 n 階矩陣 A 非奇異,則用主元高斯消去法求解Ax=b 所得到的計算解 滿足
滿足 ,其中
,其中 是單位捨入,
是單位捨入, 為主元高斯消去法的增長因子。
為主元高斯消去法的增長因子。




主元高斯消去法的數值穩定性取決於其增長因子的大小。對於部分主元高斯消去法,其增長因子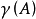 以
以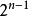 為上界。威爾金森和賴特(Wright)構造了一些例子,說明部分主元高斯消去法的增長因子的這個上界是可以達到的。但是,在大多數實際計算中,由部分主元高斯消去法所產生的矩陣元素迅速增長的情況非常罕見。
為上界。威爾金森和賴特(Wright)構造了一些例子,說明部分主元高斯消去法的增長因子的這個上界是可以達到的。但是,在大多數實際計算中,由部分主元高斯消去法所產生的矩陣元素迅速增長的情況非常罕見。
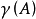
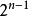
對全主元高斯消去法,威爾金森證明了 。威爾金森指出,對於充分大的 n ,這個界遠遠小於
。威爾金森指出,對於充分大的 n ,這個界遠遠小於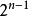 。據此可以推斷:全主元高斯消去法是數值穩定的。威爾金森曾猜測:全主元高斯消去法的增長因子以矩陣的階為界,即
。據此可以推斷:全主元高斯消去法是數值穩定的。威爾金森曾猜測:全主元高斯消去法的增長因子以矩陣的階為界,即 。但是,古爾德(Gould)構造了一個反例,說明威爾金森的猜測是不正確的。
。但是,古爾德(Gould)構造了一個反例,說明威爾金森的猜測是不正確的。